数学の問題一覧
公開日時: 2023年11月2日23:26 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
任意の二次関数$\ f\ $についてある$\ \theta \ (0\le \theta \le 2\pi)$があって,$\ xy$座標平面上で$\ y=f(x)\ $を$\ \theta \ $反時計回りに回転させたものを考える.$\ $これがある関数$\ g(x)\ $で$\ y=g(x)\ $と表せるときの$\ \theta\ $としてありうるものの総和を$\ S\ $とするとき$\ S\ $を超えない最大の整数を回答して下さい.
解答形式
整数で回答してください.
公開日時: 2022年10月19日23:33 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
角度
問題文
凸四角形$ABCD$の対角線$AC$上に点$E$があり,$\angle BAC=30^\circ$,$\angle ABE=110^\circ$,$\angle CBE=20^\circ$,$\angle DAC=10^\circ$,$\angle ADE=10^\circ$がそれぞれ成り立っている.このとき,$\angle CDE$の大きさを度数法で表すと,$x^\circ$となる.
$x$に当てはまる数を求めよ.
※3通りの解法を用意しています.難しくはないので,いろんな方向からアプローチしてみてください.
解答形式
解答のみを,半角数字で答えてください.
公開日時: 2020年6月28日18:00 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
KOH-MC
問題文
$n$ を非負整数とする。縦の長さが $3$,横の長さが $2n$ の長方形をした部屋を,辺の長さが $1$ と $2$ の長方形の畳で敷き詰める方法の総数を $a_n$ とする。ただし,部屋を固定したとき,畳を回転または反転させて一致するような敷き詰め方は区別して数える。また,便宜上 $a_0=1$ と約束する。
例えば,縦の長さが $3$,横の長さが $2$ である部屋を畳で敷き詰める方法は
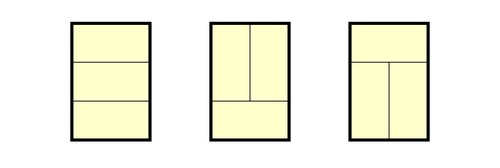 の $3$ 通りだから $a_1=3$ である。このとき
の $3$ 通りだから $a_1=3$ である。このとき
$$
a_n=\fbox{ア}\;a_{n-1}+\fbox{イ}\;\sum_{k=0}^{n-2}a_k\quad (n=2,3,\cdots)
$$が成り立つから
$$
a_4=\fbox{ウエオ}
$$である。また,上の漸化式を変形すると
$$
\lim_{n\to\infty}\frac{a_{n+1}}{a_n}=\fbox{カ}+\sqrt{\fbox{キ}}
$$が成り立つことが分かる。
解答形式
$\fbox{ア}$ 〜 $\fbox{キ}$ には,半角数字 0 - 9 のいずれかが当てはまります。$\fbox{ア}$ 〜 $\fbox{キ}$ に当てはまるものを,改行区切りで入力してください。
公開日時: 2024年3月8日21:10 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
競技数学
問題文
$\dfrac{777777777}{888888}$ は互いに素な正の整数 $a,b$ を用いて $\dfrac{a}{b}$ と表されるので,$a+b$ の値を解答してください.
解答形式
半角数字で解答してください.
公開日時: 2021年4月18日22:52 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
初等幾何 長さ

【補助線主体の図形問題 #011】
今日は傍心を登場させてみました。傍心への慣れ具合により難易度の体感が大きく変わるかもしれません。暗算でも解けるように調整してあります。存分に傍心の性質をお楽しみください。
解答形式
${
\def\cm{\thinspace \mathrm{cm}}
\def\mytri#1{\triangle \mathrm{#1}}
}$ 解答は小数第3位を四捨五入して、小数第2位までを単位なしで入力してください。
(例) $12\cm$ → $\color{blue}{12.00}$ $10\sqrt{2}\cm$ → $\color{blue}{14.14}$ $\dfrac{1+\sqrt{5}}{2} \cm$ → $\color{blue}{1.62}$
入力を一意に定めるための処置です。
たとえば答えに無理数を含む場合、$\sqrt{2}=1.41$や$\pi=3.14$などでは必要な桁が足りない場合があるのでご注意ください。
近似値を求める際には、関数電卓やグーグルの電卓機能、Wolfram|Alpha https://www.wolframalpha.com などのご利用をお勧めします。
ヒント内容の予告
- 全体の方針をぼんやりと
- ヒント1の内容をやや具体的に
- ヒント2の内容をやや具体的に
- ヒント3の続き
公開日時: 2020年6月10日17:57 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
次の命題の真偽を答えなさい。
-
$0\leq a, b < 10$ を満たす実数 $a,b$ を $10$進小数 で表したものをそれぞれ $a_0.a_1a_2a_3\cdots, \;b_0.b_1b_2b_3\cdots$ とするとき,ある $k=0,1,\cdots$ に対して $a_k\neq b_k$ ならば $a\neq b$ である。
-
$\vec{a}_1, \vec{a}_2$ を平行(*)でない平面ベクトルとする。実数 $k_1, k_2, k_1', k_2'$ に対して
\begin{equation}
k_1\vec{a}_1+k_2\vec{a}_2=k_1'\vec{a}_1+k_2'\vec{a}_2
\end{equation}が成り立つならば $k_1=k_1'$ かつ $k_2=k_2'$ である。 -
実数全体を定義域とする微分可能な実数値関数 $f(x)$ が
\begin{equation}
f'(x)=x
\end{equation}を満たすとする。このとき,$f(x)$ はある実数 $a$ を用いて
\begin{equation}
f(x)=\int_a^x t dt
\end{equation}と表せる。 -
数列 $\{a_n\}, \{b_n\}$ は $n\to\infty$ である実数に収束するとする 。任意の $n$ に対して $b_n\neq 0$ ならば,数列 $\displaystyle{\left\{\frac{a_n}{b_n}\right\}}$ も収束する。
注意
- *この問題では,平面ベクトル $\vec{a}_1, \vec{a}_2$ が平行であるとは $\vec{a}_1=k\vec{a}_2$ となる実数 $k\neq 0$ が存在することをいいます。
- (2020/6/11 15:40 更新)命題 1 の条件を変更しました。正解には影響ありません。
解答形式
$k=1,2,3, 4$ に対して,命題 $k$ が真なら T を,偽なら F を第 $k$ 行に出力してください。
公開日時: 2020年6月6日22:31 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
非負整数$n$に対し関数$f$を次のように定める。
$$f(n) = \frac{(n^2)!}{(n!)^{n+1}}$$
$1$から$2020$までの整数について$f(n)$が整数となるような$n$の個数を求めよ。
解答形式
半角数字で入力せよ。
公開日時: 2020年6月9日13:53 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
中心$O$, 直径$AB$とする円の$A,B$以外の円周上の点$C$を取り, $\angle BAC=\theta \ (0^\circ<\theta <90^\circ)$ とする。
このとき, 線分$OD$が線分$AC$によって二等分されるような点$D$が円周上に取れるような$\theta$の取りうる範囲を求めよ。
解答形式
求める$\theta$の範囲は$a^\circ<\theta\leq b^\circ$となります。1行目に$a$, 2行目に$b$を半角数字で入力してください。
公開日時: 2022年11月6日0:35 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
図の条件の下で、青で示した角の大きさ $x$ を求めてください。

解答形式
$x=a$ 度($0\leq a\lt 180$)です。整数 $a$ の値を半角数字で解答してください。
公開日時: 2023年12月30日3:03 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
$8\times 8$のマス目に$1\times 2$のタイルと$1\times 1$のタイルを隙間なく並べる方法のうち,以下の条件を満たすものを考えます.
- どの行にも$1\times 1$のタイルがちょうど$1$つ含まれる.
このような並べ方のうち,横向きの$1\times 2$のタイルの個数が最大となるものは何通りありますか?
ただし,回転や裏返しによって一致する並べ方は区別します.また,$1\times 2$のタイルが横向きであるとは,長辺が行に平行であることを指します.
解答形式
半角数字で入力してください.
公開日時: 2020年6月28日18:00 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
KOH-MC
問題文
$x$ についての2次方程式
$$
3x^2+(5k-4)x+4k = 0
$$が異なる2つの正の実数解 $\alpha,\beta\;(\alpha<\beta)$ を持ち、$\beta$ の小数部分が $\alpha$ である。このとき、$k$ の値を求めよ。
解答形式
解答は
$$
\frac{N-\sqrt{M}}{L}
$$と表わされる($N,M,L$ は自然数)。分数や平方根は最も簡単な形にしてある。解答欄には $N, M, L$ の値をそれぞれ 1, 2, 3 行目に半角数字で入力せよ。