数学の問題一覧
問題文
$n^9$ と $n^{25}$ の $1$ の位が等しいような $1$ 桁の正整数 $n$ を全て求め、それらの総和を解答してください。
解答形式
半角数字で解答してください
問題文
同一平面上に $2$ 円 $\omega_{1},\omega_{2}$ があり、相異なる$2$ 点 $A,B$ で交わっています。$A$ における $\omega_{2}$ の接線を $l_{A}$ 、$B$ における $\omega_{1}$ の接線を$l_{B}$ とし、$l_{A}$ と $l_{B}$ の交点を $X$ とします。また、$l_{A}$ と $\omega_{1}$ の交点のうち、$A$ でない点を $C$、$l_{B}$ と $\omega_{2}$の交点のうち、$B$ でない点を $D$ とすると、$A,C,X$ はこの順に同一直線上にあり、以下が成立しました。
$$XB=9 BC=2 AD=5$$
このとき、線分 $BD$ の長さを求めてください。
なお、$\omega_{2}$ の半径の方が $\omega_{1}$ の半径より大きいことが保証されます。
解答形式
$BD$ の長さは互いに素な整数 $a,b$ を用いて $\dfrac{a}{b}$ と表されるので、$a+b$ を解答してください。
問題文
$AB=10,BC=21,CA=17$ をみたす三角形 $ABC$ の内心を $I$ とします。辺 $AB$ 上に点 $D$ をとると、直線 $DI$ が三角形 $ABC$ の面積を $2$ 等分し、さらに辺 $BC$ と交わりました。このときの線分 $AD$ の長さを求めてください。
解答形式
$AD$ の長さは正整数$a,b$を用いて $\sqrt{a}-b$ と表されるので、$a+b$ を解答してください
問題文
相異なる $1$ 以上 $9$ 以下の整数の組 ($A,E,M,S,T,U,Y$) が以下の覆面算を満たしています
$$\begin{array}{rr}
& MATU \\
+ & YAMA \\
\hline
& EAST
\end{array}$$
このとき、$EAST$ としてありうる値を見つけてください。
解答形式
$EAST$ としてありうる値が$3$つ存在するので、それらの総和を解答してください。
問題文
複素数$\alpha,\beta,\gamma$が
$$\begin{cases}
\alpha+\beta+\gamma=9\\
\alpha^2+\beta^2+\gamma^2=25\\
\alpha^3+\beta^3+\gamma^3=2025
\end{cases}$$
を満たしています。このとき、$f(x)=0$ が $\alpha,\beta,\gamma $を解に持ち、かつ最高次係数が $1$ であるような $3$ 次関数 $f(x)$ が一意に存在するので、$❘f(2)❘$ を求めてください。
解答形式
解答は正の整数値になるので、その値を解答してください
問題文
$2025 \times 2025$ のマス目があり、右から $m$ 列目、上から $n$ 行目のマスを $(m,n)$ と表します。
いま、$(1,1)$ に東くんがおり、辺を共有するマスを通って最短距離で $(2025,2025)$ まで移動します。
このとき、以下を満たすような移動方法は $M$ 通りあります。$M$ は $2$ で何回割り切れますか?
$$i と j がともに偶数であるようなマス (i,j) を一つも通らない$$
解答形式
半角数字で解答してください
問題文
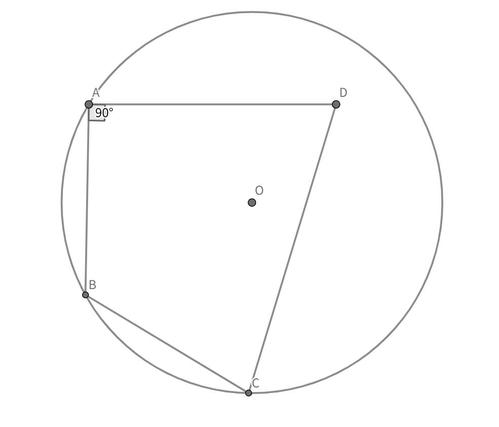
以下のように点 $O$ を中心とする円周上に三角形 $ABC$ が内接しています。この円の内部に点 $D$ を取ると、$AB=BC=AO=4,\angle BAD=90°$ が成り立ち、さらに三角形 $AOD$ の面積は $3\sqrt{3}$ でした。このときの線分 $CD$ の長さの $2$ 乗を求めてください。
解答形式
解答は正の整数値になるので、その値を半角数字で解答してください
問題文
ある三角形は内接円の半径が $9$、外接円の半径が $25$、傍接円の一つの半径が $\sqrt{2025}$ です。この三角形の面積を求めてください
解答形式
解答は正の整数値になるので、その値を解答してください。
問題文
$2025年9月25日$ のように、西暦、年、日が全て平方数であるような日をEMOい日とします。
$2025年9月25日$ の次のEMOい日は $a年b月c日$ です。$a+b+c$ を解答してください
解答形式
半角数字で解答してください
問題文
$AB=BC$で、面積が$2025$であるような二等辺三角形$ABC$がある。$AB(=BC)$の最小値を求めよ。
解答形式
半角数字で$AB^2(=BC^2)$の値を入力してください。
問題文
次の文章の$\fbox{1},\dotsc,\fbox{6}$に当てはまる数を求めよ。
$$
a_{n} = \int_{1}^{e^{0.1}}(\log{x})^{n}dx \qquad (n=0,1,2,\dotsc)
$$とする。部分積分法を用いることで,漸化式
$$
a_{n} = (\fbox{1})^{n}\cdot e^{\fbox{2}} - na_{n-1} \qquad (n\geq1)
$$を得る。$a_{3}$は,有理数$\fbox{3},\fbox{4}$を用いて
$$
a_{3} = \fbox{3}e^{\fbox{2}}+\fbox{4}
$$と表せる。$1\leq x\leq e^{0.1}$のとき$0\leq(\log{x})^{n}\leq0.1^{n}$より$0\leq a_{n}\leq(e^{0.1}-1)\cdot0.1^{n}$である。$n=3$に対してこの不等式を用いることにより$e^{-0.1}$を小数点第4位まで求めることができる。$e^{-0.1}$の小数点第5位以下を切り捨てた小数点第4位までの値は$\fbox{5}$である。
また,$\displaystyle b_{n}=\frac{(-1)^{n}e^{-0.1}}{n!}a_{n}$とすることで$a_{n},b_{n}$の一般項は容易に求められる。
$$
0 \leq |b_{n}| = \frac{e^{-0.1}a_{n}}{n!} < \frac{1-e^{-0.1}}{10^{n}\cdot n!}
$$より,はさみうちの原理から$\displaystyle\lim_{n\to\infty}|b_{n}| = 0$,つまり
$$
\sum_{n=0}^{\infty}\frac{(-0.1)^{n}}{n!} = e^{\fbox{6}}
$$が求められる。
解答形式
$\mathrm{i}=1,\dotsc,6$に対し,$\fbox{i}$に当てはまる数を$\mathrm{i}$行目に半角で答えてください。例えば,$\fbox{1},\dotsc,\fbox{6}$にそれぞれ$1.2,3.45,-6,7.89,1.2356,-2.3$が当てはまるときは
1.2
3.45
-6
7.89
1.2356
-2.3
と解答してください。