全問題一覧
公開日時: 2025年11月11日20:40 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
関数方程式
問題文
次を満たす整数係数多項式の組 $(f,g)$ はいくつありますか?
$$f(g(x))=x^6+1 0≦f(0),g(0)≦2025$$
解答形式
条件を満たす組の個数を半角整数で $1$ 行目に入力してください。
公開日時: 2025年11月10日20:52 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
$ $ $0$ 以上 $9$ 以下の整数 $a, b, c, d$ に対し,数列 $(x_0, x_1, ..., x_{1110})$ を次のように定めます:
- $x_0 = a$ である.
- $(x_0, x_1, ..., x_{10})$ は公差 $b$ の等差数列をなす.
- $(x_{10}, x_{11}, ..., x_{110})$ は公差 $c$ の等差数列をなす.
- $(x_{110}, x_{111}, ..., x_{1110})$ は公差 $d$ の等差数列をなす.
$x_{1110}$ のとり得る値の総和を求めて下さい.
解答形式
答えは非負整数値であることが保証されます.半角英数にし,答えとなる非負整数値を入力し解答して下さい.
公開日時: 2025年11月9日12:27 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
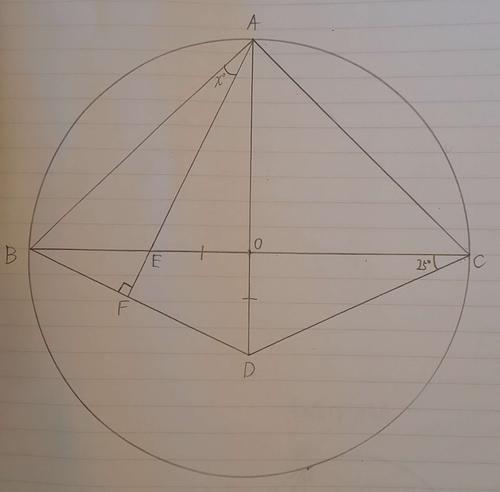
円Oの直径BCを斜辺とし、円周上に点Aを取った三角形ABCと、線分AOを少し延長したところに点Dを取った三角形BCDがある。そこに、∠Aから辺BDに垂直な線分を書き、その交点を点Fとした。EO=DO,∠OCD=25°のとき、∠BAFは何度ですか。
解答形式
例)〇〇°
公開日時: 2025年11月1日12:52 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
奇数回で当たる確率が $\dfrac{2}{n}$,偶数回で当たる確率が $\dfrac{3}{n}$のくじを$n$回引いた時,少なくとも1回当たる確率を $P_n$,1回以上当たった時,最初の当たりが奇数回で起こる確率を $Q_n$ とするとき,$\displaystyle\lim_{n\to\infty}Q_n$ を求めてください.
解答形式
求める値は互いに素な正整数 $a, b$ を用いて $\dfrac{a}{b}$ と表せるので, $a+b$ を解答してください. 数字は半角で入力してください.
公開日時: 2025年11月1日0:00 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 採点者ジャッジ
第1問
次の空欄$(ア)~(オ)$に当てはまる数字をそれぞれ答えよ。
数列{$a_{n}$}を次のように定める。
$$a_1=a_2=1,a_{n+2}-a_{n+1}+a_n=0 (nは自然数)$$この数列の一般項は
$a_n=\frac{(ア)}{\sqrt{(イ)}}$$sin\frac{nπ}{(ウ)}$
である。
また、$a_{2025}=(エ)$であり、$$\sum_{n=1}^{2025}{a_n}=(オ)\quad$$である。