数学の問題一覧
問題文
二等辺三角形ABCがあり、AB=AC=xcmである。また、頂角は150°である。下の式が二等辺三角形ABCの面積の値と等しくなった時、xの数値を求めなさい。(・は掛け算の×を表しています)
$$
\frac{x^4-10x^2+9}{(x+1)(x+3)(x-3)} + \sqrt{25+4\sqrt{6}} \cdot \sqrt{25-4\sqrt{6}} + \frac{(x+2)^3-(x-2)^3}{12x} + \frac{\sqrt{2}}{\sqrt{3}+\sqrt{1}} + \frac{\sqrt{2}}{\sqrt{5}+\sqrt{3}} + \frac{\sqrt{2}}{\sqrt{7}+\sqrt{5}} - \frac{\sqrt{14}}{\sqrt{2}} + 19
$$
解答形式
x=は必要ありません。数値のみを記入してください
(例) 810
問題文
三角形ABCの
Pを線分AB上にABを2:3に内分するように、
Qを直線BC上にBCを1:2に外分するように、
Rを直線AC上に取ったところ、
P,Q,Rは一直線上にありました
この時、AR/CRの値を求めてください。
解答形式
解答する値は互いに素な自然数(a,b)を用いてa/bと表せるので、a+bの値を求めてください
問題文
円に内接する四角形 $ABCD$ があり,$\angle ABC = 90^\circ$ をみたしている.$2$ 点 $A , C$ を通り直線 $AB$ に接するような円と線分 $BD$ の交点を $E$ とすると,$CD = CE$ が成立した.$BE = 7 , ED = 9$ であるとき,線分 $AB$ の長さの2乗を求めよ.
解答形式
半角数字で解答してください.
問題文
$AB=44,AC=46$ をみたす三角形 $ABC$ があり, $AB,AC$ の中点を $M,N$ とする. 三角形 $ANB$ の外接円と三角形 $AMC$ の外接円の $A$ でない交点を $P$ とすると $P$ が線分 $BC$ 上に存在した.
このときの線分 $BC$ の長さを求めよ
解答形式
$BC^2$ は正の整数値になるので, その値を半角で解答してください
問題文
$y=xe^x$の第$n$次導関数を$y^{(n)}$とし,
そのグラフの変曲点の$y$座標を$Y_{n+1}$とおく。
$\sum_{k=1}^{\infty} Y_k$
を求めよ。ただし,答えのみ記せ。
問題文
「正方形と正三角形 Part1」に続いており、誘導のようになっているため、Part1を解いていない方は先にPart1を解いておくことをお勧めします♪
誘導なしでもデキルケド、、、
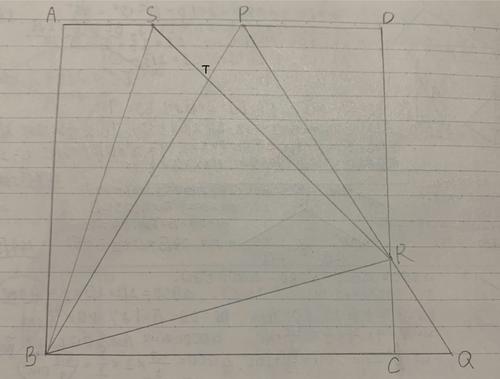
四角形ABCDは正方形である。辺AD上に点P、BCの延長線上に点Qを取ると、三角形PBQは正三角形になる。DCとPQの交点をRとする。AP上にSを取ると三角形SBRも正三角形になる。次の問いに答えなさい。
SRとPBの交点をTとする。SBはSTの何倍であるか答えなさい。
解答形式
◯倍のような「倍」はつけずに数字や記号のみで答えてください。√、+、-などを使う場合はカタカナで表記してください。2+√2のように、√の数よりも先に2などの整数を答えてください。√同士であれば、中身の数が少ない順に答えなさい。
√→ルート
+→プラス
-→マイナス
(例)3
2ルート3
3マイナスルート2プラスルート3
問題文
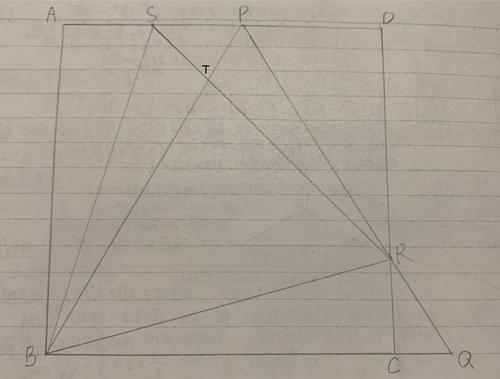
四角形ABCDは正方形である。辺AD上に点P、BCの延長線上に点Qを取ると、三角形PBQは正三角形になる。DCとPQの交点をRとする。AP上にSを取ると三角形SBRも正三角形になる。次の問いに答えなさい。
角RBCの大きさを求めなさい
解答形式
角度の大きさは数字のみで回答してください
(例)180
90 など
問題文
長方形ABCDがあり、AB=X cm、AD=Ycmとする。(X:Y=1:2)
CB=CEとなるよう、AD上に点Eをとる。
点Pは頂点Bから頂点Cまで動く。
CEとPDの交点をSとする。
このとき、三角形CBE相似三角形EPSになるような場所に点Pがあるとき、次の(ア)〜(ウ)にはいる数字を答えなさい。
BP:PC=(ア):√(イ)+(ウ)
解答形式
ア、イ、ウの順に、間に点を入れながら答えてください。1行で答えること。
(例)
1、2、3