GaLLium31

問題文

正整数に対して定義され非負整数値をとる関数 $f$ が以下を満たしています．

• 任意の正整数 $x,y$ について $f(xy)=f(x) \oplus f(y)$

• $x$ と $y$ が互いに素ならば $f(xy)=f(x)+f(y)$

このような関数 $f$ について，以下を満たす正整数の組 $(x,y)$ の個数を $c(f)$ とします．$c(f)$ がとりうる値は有限個なので，その総和を解答してください．

• $x,y$ はともに $30^{10}$ の約数である．

• $f(xy)=f(x)+f(y)$

追記: $\oplus$ はビットごとの排他的論理和です

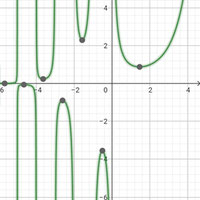
問題文

平方因子を持たない正整数 $n$ であって，$\dfrac{\phi(n)}{\gcd(n,\phi(n))} = 18$ を満たすものの総和を解答してください．

問題文

$30$ の正の約数を並べ替えた数列 $A$ としてありうるもの全てに対する，以下の操作方法の個数の総和を解答してください．

• 「連続する $2$ 数 $A_i,A_{i+1}$ であって $A_i \mid A_{i+1}$ を満たすものを $1$ つ選び，それらをともに $A$ から削除する」という操作を $4$ 回行い，$A$ を空にする．

問題文

$S=\lbrace 0,1, \ldots , 30 \rbrace$ とします．関数 $f:S \rightarrow S$ であって，以下を満たすようなものの個数を $N$ とします．

• 任意の $x,y \in S$ について，$x^{12}-y^{12}$ が $31$ の倍数ならば，$f(x)^{25}-f(y)^{25}$ も $31$ の倍数．

$N = a \cdot b^c$ であるような正整数 $a,b,c$ について，$a+b+c$ の最小値を解答してください．

問題文

正整数 $a$ に対して，$\dfrac{n(n+2)}{a}$ が平方数であるような正整数 $n$ が無限に存在しました．さらに小さい方から $i$ 番目のものを $n_i$ とすると，任意の正整数 $i$ が $n_{i+2}+n_{i}=98n_{i+1}+2n_1$ を満たしました．このとき，$a$ としてありうるものの総和を解答してください．

問題文

$60$ 以下の正整数 $n$ に対して，それを $2,3,4,5$ で割ったあまりをそれぞれ $a,b,c,d$ とします．$xy$ 平面上に $P(a,b)$ と $Q(c,d)$ をとったとき $PQ= 1$ となるような $n$ の個数を解答してください．

問題文

$\dfrac{51-n}{n-1}$ が平方数となるような整数 $n$ の総和を解答してください．

(13:17追記　 $0$ も平方数に含むとします)

問題文

上から $i$ 段目 $(1 \leq i \leq 2026)$ に $i$ 個の正整数を並べて三角形を作る方法であって，どの段も総和が $2026$ となるようなものの個数を素数 $2029$ で割ったあまりを解答してください．

問題文

$ \pi$ ナポゥくんの生まれた日からの日数を $N$ とします.
$ \pi$ ナポゥくんは既に $3$ 歳の誕生日を迎えていますが，$28$ 歳の誕生日は迎えていません．
$N$ の各桁の総和が $22$ であるとき、$N$ として考えられる正整数はいくつありますか．

解答形式

半角英数字で解答してください．

問題文

正三角形 $ABC$ の内部を以下のように歩く移動するペンギンがいる．

・ 常に直進するが，辺（頂点を除く）にぶつかった場合は，辺に対して今移動してきた直線と対称な直線へ方向転換する．頂点についた場合，その時点で歩行をやめる．

また，$0\leq p \leq 1$を満たす実数 $p$ に対して，$f(p)$を以下のように定める．

・$f(p)$は，$AC$ を $p:1-p$ に内分する点を $D$ とし，このペンギンがはじめ $B$ にいて、$D$ に向かって直進したときの，ペンギンの歩行が止まるまでに辺（頂点を除く）にぶつかった回数

正整数 $n$ に対して，$f(p)=n$ を満たす $p$ の総和が $9$ であったとき，$n$ としてありうる値の総積を求めてください．

解答形式

非負整数を半角英数字で解答してください．

問題文

実数係数多項式で次数が $9999$ 以下の $P(x)$ について，$(P(1),P(2), \dotsc P(10000))$ が $(1,2, \dotsc 10000)$ の並べ替えであるとき，$P(10001)$ が考えられる最大値をとるような $P(x)$ の個数を素数 $9973$ で割ったあまりを解答してください．

解答形式

半角数字で解答してください．

問題文

$30$ 人の人が $\pi$ ナポゥ君の主催するたけのこニョッキ大会に参加します．ルールは次の通りです．

• $i=30,29, \dotsc,1$ の順に $1$ 人 $1$ つの数 $i$ を叫んでいき，最後まで叫ぶことができたら成功である．もし $i$ を複数人が叫んでしまったり，だれも叫ばなかったりした場合は失敗である．

なかなか成功しないことに気づいた $\pi$ ナポゥ君は，次のように八百長をすることにしました．

• はじめに $30$ 人それぞれに正整数を与え，$i=30,29,\dotsc,1$ について以下を繰り返す．
  • まだ叫んでいない人の内，与えられた数が $i$ の約数もしくは倍数である人は，数 $i$ を叫ぶ．

このたけのこニョッキが成功するような，$30$ 人に与えられる正整数の総和の最小値を解答して下さい．

解答形式

半角数字で解答してください．

問題文

正整数 $n$ に対して $n^{10n}$ を $31$ で割ったあまりを $f(n)$ としたとき，
$$\sum_{k=1}^{12000} f(k)$$
の値を求めてください．

解答形式

半角英数字で回答してください．