正方形と正三角形　Part2

問題文

「正方形と正三角形　Part1」に続いており、誘導のようになっているため、Part1を解いていない方は先にPart1を解いておくことをお勧めします♪
誘導なしでもﾃﾞｷﾙｹﾄﾞ､､､

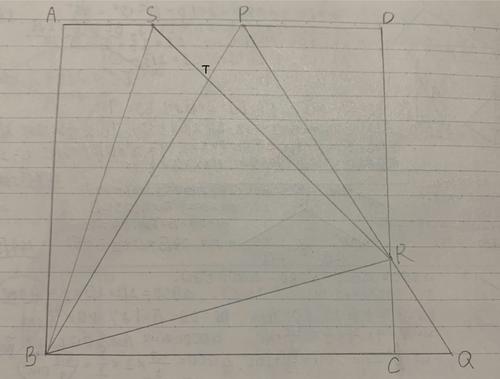
四角形ABCDは正方形である。辺AD上に点P、BCの延長線上に点Qを取ると、三角形PBQは正三角形になる。DCとPQの交点をRとする。AP上にSを取ると三角形SBRも正三角形になる。次の問いに答えなさい。

SRとPBの交点をTとする。SBはSTの何倍であるか答えなさい。

解答形式

◯倍のような「倍」はつけずに数字や記号のみで答えてください。√、+、-などを使う場合はカタカナで表記してください。2+√2のように、√の数よりも先に2などの整数を答えてください。√同士であれば、中身の数が少ない順に答えなさい。
√→ルート
+→プラス
-→マイナス
(例)3
　　2ルート3
　　3マイナスルート2プラスルート3