数学の問題一覧
問題文
「正方形と正三角形 Part1」に続いており、誘導のようになっているため、Part1を解いていない方は先にPart1を解いておくことをお勧めします♪
誘導なしでもデキルケド、、、
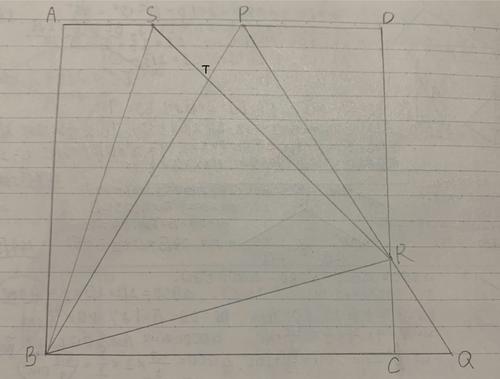
四角形ABCDは正方形である。辺AD上に点P、BCの延長線上に点Qを取ると、三角形PBQは正三角形になる。DCとPQの交点をRとする。AP上にSを取ると三角形SBRも正三角形になる。次の問いに答えなさい。
SRとPBの交点をTとする。SBはSTの何倍であるか答えなさい。
解答形式
◯倍のような「倍」はつけずに数字や記号のみで答えてください。√、+、-などを使う場合はカタカナで表記してください。2+√2のように、√の数よりも先に2などの整数を答えてください。√同士であれば、中身の数が少ない順に答えなさい。
√→ルート
+→プラス
-→マイナス
(例)3
2ルート3
3マイナスルート2プラスルート3
問題文
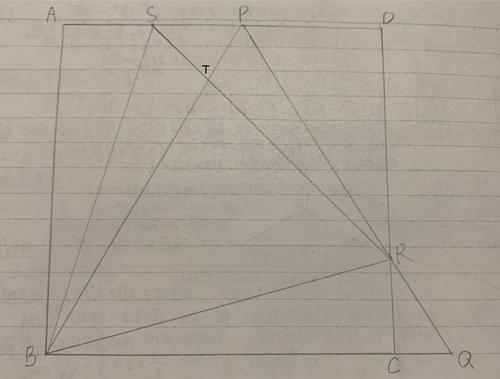
四角形ABCDは正方形である。辺AD上に点P、BCの延長線上に点Qを取ると、三角形PBQは正三角形になる。DCとPQの交点をRとする。AP上にSを取ると三角形SBRも正三角形になる。次の問いに答えなさい。
角RBCの大きさを求めなさい
解答形式
角度の大きさは数字のみで回答してください
(例)180
90 など
問題文
長方形ABCDがあり、AB=X cm、AD=Ycmとする。(X:Y=1:2)
CB=CEとなるよう、AD上に点Eをとる。
点Pは頂点Bから頂点Cまで動く。
CEとPDの交点をSとする。
このとき、三角形CBE相似三角形EPSになるような場所に点Pがあるとき、次の(ア)〜(ウ)にはいる数字を答えなさい。
BP:PC=(ア):√(イ)+(ウ)
解答形式
ア、イ、ウの順に、間に点を入れながら答えてください。1行で答えること。
(例)
1、2、3
問題文
長方形ABCDがあり、AB=Xcm、AD=Ycmである。 (X <Y) 点Pは頂点Bを出発して頂点Cまで動く。
途中、角APDが直角になった時が2回あった。
ここで、1回目に直角になった時の点Pの位置をQとし、2回目に直角になった時の点Pの位置をRとする。
BQ=2cm、QR=4cmである時、X、Yはそれぞれ何cmだと考えられるか?
解答形式
下の形式のようにX、Yは大文字、cmは小文字で、2行構成で答えなさい。ただし√が含まれる場合はカタカナで答えなさい。
√2→ルート2
5√17→5ルート17
(例)
Xcm=◯◯cm
Ycm=◯◯cm
${}$ 西暦2026年問題第10弾です。今年の最終回を迎えました。最終回はどこから手を付けていいのか迷ういそうな問題を用意しています。とはいえ、タネに気づけばサクッと解けるように仕込んであります。じっくりと腰を据えてお楽しみください。
解答形式
${}$ 解答は求める$x$の値を小さい順に2行に分けて半角で入力してください。「$x=$」の記載は不要です。
(例)$x=$110, 2026 → 《1行目》$\color{blue}{110}$、《2行目》$\color{blue}{2026}$
${}$ 西暦2026年問題第8弾です。$2026$を$2^{26}$とする強引な西暦問題となりました。ついでに書くと、どこかに類題がありそうで、その点でも恐れています。皆さんはそんな僕の恐れなど気にせずにお楽しみください。
解答形式
${}$ 解答は1行目に$p_3$の値を、2行目に$p_4$の値を、それぞれ半角で入力してください。「$p_3=$」「$p_4=$」といった記載は不要です。
(例)$p_3=$108、$p_4=$2026 → 《1行目》$\color{blue}{108}$、《2行目》$\color{blue}{2026}$
${}$ 西暦2026年問題第7弾です。見た目も実際もがっつり整数問題です。ひととき整数と戯れてみてください。
なお、$2026$より大きい整数の素数判定が待ち受けています。適宜、素数表(たとえば https://en.wikipedia.org/wiki/List_of_prime_numbers )を利用するなり、Wolfram|Alpha( https://www.wolframalpha.com )を利用するなりしてください。
解答形式
${}$ 解答は求める値をそのまま半角で入力してください。
(例)107 → $\color{blue}{107}$
求められているのは平方数と素数に挟まれた数であることに注意してください。





