数学の問題一覧
公開日時: 2025年9月25日21:00 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
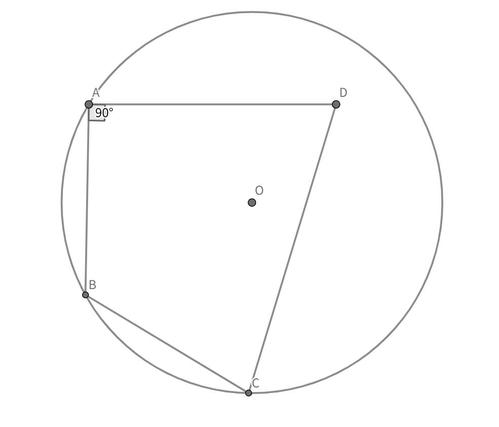
以下のように点 $O$ を中心とする円周上に三角形 $ABC$ が内接しています。この円の内部に点 $D$ を取ると、$AB=BC=AO=4,\angle BAD=90°$ が成り立ち、さらに三角形 $AOD$ の面積は $3\sqrt{3}$ でした。このときの線分 $CD$ の長さの $2$ 乗を求めてください。
解答形式
解答は正の整数値になるので、その値を半角数字で解答してください
公開日時: 2025年9月25日21:00 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
$a,b$ を $a \le b$ を満たす正の整数とします。
$2025\times 2026$ のマス目があります。ここに $a\times b$ のタイルを何枚か置くことでマス目を隙間なく敷き詰めることが出来ました。
このような $(a,b)$ の組はいくつありますか?
追記 タイルは回転してかまいません。
解答形式
半角数字で解答してください
公開日時: 2025年9月25日21:00 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
ある三角形は内接円の半径が $9$、外接円の半径が $25$、傍接円の一つの半径が $\sqrt{2025}$ です。この三角形の面積を求めてください
解答形式
解答は正の整数値になるので、その値を解答してください。
公開日時: 2025年9月25日21:00 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
相異なる $1$ 以上 $9$ 以下の整数の組 ($A,E,M,S,T,U,Y$) が以下の覆面算を満たしています
$$\begin{array}{rr}
& MATU \\
+ & YAMA \\
\hline
& EAST
\end{array}$$
このとき、$EAST$ としてありうる値を見つけてください。
解答形式
$EAST$ としてありうる値が$3$つ存在するので、それらの総和を解答してください。
公開日時: 2025年9月25日21:00 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
$n^9$ と $n^{25}$ の $1$ の位が等しいような $1$ 桁の正整数 $n$ を全て求め、それらの総和を解答してください。
解答形式
半角数字で解答してください
公開日時: 2025年9月25日21:00 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
複素数$\alpha,\beta,\gamma$が
$$\begin{cases}
\alpha+\beta+\gamma=9\\
\alpha^2+\beta^2+\gamma^2=25\\
\alpha^3+\beta^3+\gamma^3=2025
\end{cases}$$
を満たしています。このとき、$f(x)=0$ が $\alpha,\beta,\gamma $を解に持ち、かつ最高次係数が $1$ であるような $3$ 次関数 $f(x)$ が一意に存在するので、$❘f(2)❘$ を求めてください。
解答形式
解答は正の整数値になるので、その値を解答してください
公開日時: 2025年9月25日21:00 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
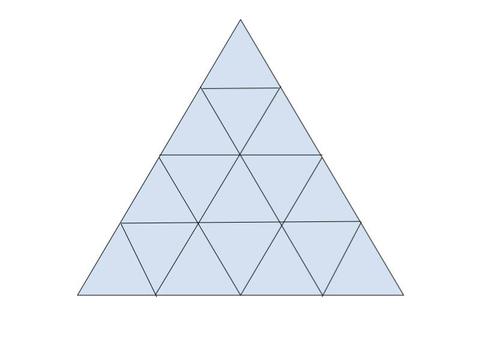
一辺の長さが $4$ の正三角形を、以下のように一辺の長さが $1$ の小正三角形 $16$ 個に分割します。
東くんがこの小正三角形それぞれに $0,1,2$ のいずれか一つを書き込むと、辺を共有して隣り合う $2$ つの小正三角形に書かれた数の差(の絶対値)はすべて $1$ でした。
このように東くんが書き込む方法は何通りありますか?ただし裏返しや回転によって一致する書き込み方も区別します。
解答形式
半角数字で解答してください
公開日時: 2025年9月25日21:00 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
$2025年9月25日$ のように、西暦、年、日が全て平方数であるような日をEMOい日とします。
$2025年9月25日$ の次のEMOい日は $a年b月c日$ です。$a+b+c$ を解答してください
解答形式
半角数字で解答してください
公開日時: 2025年9月25日21:00 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
同一平面上に $2$ 円 $\omega_{1},\omega_{2}$ があり、相異なる$2$ 点 $A,B$ で交わっています。$A$ における $\omega_{2}$ の接線を $l_{A}$ 、$B$ における $\omega_{1}$ の接線を$l_{B}$ とし、$l_{A}$ と $l_{B}$ の交点を $X$ とします。また、$l_{A}$ と $\omega_{1}$ の交点のうち、$A$ でない点を $C$、$l_{B}$ と $\omega_{2}$の交点のうち、$B$ でない点を $D$ とすると、$A,C,X$ はこの順に同一直線上にあり、以下が成立しました。
$$XB=9 BC=2 AD=5$$
このとき、線分 $BD$ の長さを求めてください。
なお、$\omega_{2}$ の半径の方が $\omega_{1}$ の半径より大きいことが保証されます。
解答形式
$BD$ の長さは互いに素な整数 $a,b$ を用いて $\dfrac{a}{b}$ と表されるので、$a+b$ を解答してください。
公開日時: 2025年9月25日21:00 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
$AB=10,BC=21,CA=17$ をみたす三角形 $ABC$ の内心を $I$ とします。辺 $AB$ 上に点 $D$ をとると、直線 $DI$ が三角形 $ABC$ の面積を $2$ 等分し、さらに辺 $BC$ と交わりました。このときの線分 $AD$ の長さを求めてください。
解答形式
$AD$ の長さは正整数$a,b$を用いて $\sqrt{a}-b$ と表されるので、$a+b$ を解答してください
公開日時: 2025年9月25日21:00 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
$$9^a=2^b+5^c$$
を満たす非負整数の組 $(a,b,c)$ を全て求めてください。
解答形式
$(a,b,c)$ としてありうる組すべてについて、$a+b+c$ の総和を解答してください