全問題一覧

$$
f(m)=|\quad{\sqrt{{m}^{log_{3}{9}}+log_{m}{m}+2log_{4}{4}^m}}|\\について、m<-1のとき、f(3)を求めて下さい。
$$
$$
(1)-4(2)-3(3)-2(4)-1
$$

問題文

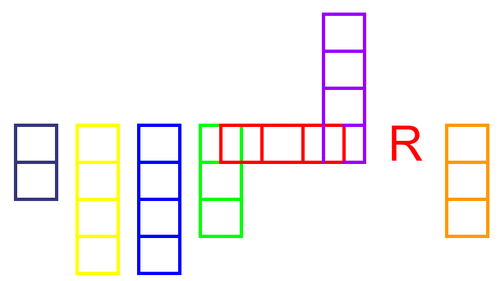
① -2019/9/1 100
② 2019/11/10 10th
③ 2020/11/11 11-12
この人達が踊っている動画は？

解答形式

タイトル

問題文

下式を満たす自然数(a,b,c)の組をすべて求めよ。
$$
2^{a}+3^{b}=5^{c}
$$
出題者も絞り込みがうまくできず難航していますのでできましたら解法もセットでご教授ください。

解答形式

(a,b,c)の形で答えてください。

(1). $(1+x)^\alpha\ (\alpha\in{\mathbb{R}})$のマクローリン展開を求めよ.
(2). $\arcsin{x}$のマクローリン展開を求めよ.

$$
|tan2250°・cos1800°・sin1200°|\\を求めて下さい。
$$
$$
(1)\frac{1}{2}(2)\frac{\sqrt{3}}{2}(3)1(4)2
$$

問題文

謎を解いて英単語を導き出そう
(写真を付け忘れていたので再投稿)

解答形式

全角英語大文字で入力してください。

You can not pick (α) this problems every day.
$$
(α)に当てはまる適語を答えて下さい。
$$

(1)into
(2)off
(3)out
(4)at

問題文

問一
このもんだいぶんはめたこ
うぞうがちになります。ぜ
んたいのかたちがじゅうに
かけるじゅうにのせいほう
けいになっていてこのもん
だいぶんをたてかけるよこ
をはちかけるじゅうはち、
きゅうかけるじゅうろくに
それぞれしなおし、「ち」
のしたのもじを、つぎのも
んだいのきごうにこのぶん
のとおったじゅんにはめる

問二
覆面算です。同じひらがなには同じ数字があてはまり、異なるひらがなに同じ数字は入りません。ただし、「」内の言葉に同じひらがなはない。（少しずれてしまっているのは申し訳ないです。）

・　　　　F D　　　　　Ｂ J　　
　　　　×Ｉう　　　　　×め
　　――――――　　――――
　　　　H G う　　　「　　　」
　　 ほ け C　　　　 　↑　出来たひらがな３文字を次の問題の「」にいれろ
　　―――――
　　ほ Ａ E う

問三
同じ矢印は同じ行動をする。五十音表を見ながらやることをおすすめします。
五十音表　　　　　　わらやまはなたさかあ
　　　　　　　　　　をり　みひにちしきい
　　　　　　　　　　んるゆむふぬつすくう
　　　　　　　　　　　れ　めへねてせけえ
　　　　　　　　　　　ろよもほのとそこお

「」→⇒⇒⇒ひにち　　「」⇨→→➤ちいき　　　きすう☞⇒➤➤につけ
さかな➤→⇨かたな　　　かおす⇒➤→⇨こたつ　　こけい➤➤→けいと
はのい☞→のうは　のとき、

「」⇨→☞☞⇒⇒→➤➤➤➤➤→➤→＿＿＿

ラスト謎

答えは、正方形で「＿＿＿」にすると？

解答形式

ひらがな二文字で入力してください。

問題文

問題に不備がある可能性があるため、他の問題を先に解くことをおすすめします。申し訳ございません。ただいま確認作業を行っております。（18:31）

グラフとは，頂点集合とそのうち $2$ 点を結ぶ辺の集合のことである。今回は単純グラフ（同じ頂点を結ぶ $2$ 辺が存在しない場合）のみを考える。

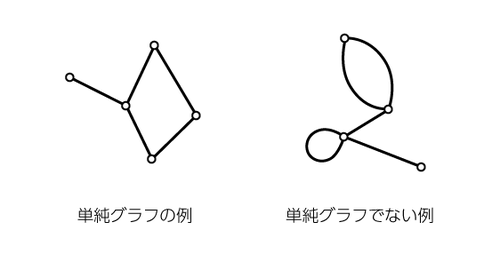
$2n$ 頂点で三角形が存在しない，すなわちどの頂点集合 ${a, b, c}$ を選んでもすべてが辺によって結ばれていることはないようなグラフの辺数の最大値を求めよう。

まず，各頂点 $i\;(i=1,2,\cdots, 2n)$ に $\displaystyle{\sum_{i=1}^{2n}}v_i=1$ となるように非負実数 $v_i$ を割り当てる。この制約のもとで，

$$
S:=\sum_{\substack{\{i,j\}が辺で \\ 結ばれている}} v_iv_j
$$

を最大化することを考える（編注：和は辺で結ばれている頂点 $i, j\;(1\leq i < j\leq 2n)$ すべてにわたることを意味する）。

$$
X_x:=\sum_{\substack{\{x,i\}が辺で \\ 結ばれている}} v_i
$$

とする。次のような操作をくり返す。

操作
辺によって結ばれていない $2$ 頂点 $i,j$ について，$\fbox{ア}$ ならばある正の実数 $\varepsilon$ を選んで $v_i \mapsto v_i+\varepsilon$，$v_j\mapsto v_j-\varepsilon$ という置き換えを行う。ただし $\varepsilon$ は置き換え後も $v_1+\cdots+v_{2n}=1$ かつ $v_1, \cdots, v_{2n}\geq 0$ が成り立つようにとる。

操作をくり返すと，$(X_i+\varepsilon)v_i+(X_j-\varepsilon)v_j$ と $X_iv_i+X_jv_j$ の値を比較することで $S$ は必ず $\fbox{イ}$ ことが分かる。これ以上操作を行っても $S$ の値が変化しないような状態に達したときを考えると，$\fbox{ウ}$ となるような任意の $2$ 点 $i,j$ どうしは辺で結ばれている。グラフが三角形を含まないことから，このとき

$$
S\leq \fbox{エ}
$$

である（編注：等号が成立するグラフが存在するように選ぶこと）。はじめ，すべての $v_i$ が等しかったとすると，操作を行う前は

$$
S=\frac{（辺の本数）}{\fbox{オ}}
$$

なので，（辺の本数）$\leq \fbox{カ}$ が分かる。

等号は $2n$ 頂点が $n$ 頂点の組 $2$ つに分かれていて，異なる組に属している場合のみ辺が存在するようなグラフで成り立つ。よって最大の辺数は $\fbox{カ}$ である。

$\fbox{ア}$ 〜 $\fbox{カ}$ に最もよく当てはまるものを，次の選択肢の中からそれぞれ選びなさい。

選択肢

$\fbox{ア}$ の選択肢：

1$\;v_i\leq v_j$　2$\;v_i\geq v_j$　3$\;X_i\geq X_j$　4$\;X_i\geq X_j$

$\fbox{イ}$ の選択肢：

1 変化しないか増加する　2 変化しないか減少する

$\fbox{ウ}$ の選択肢：

1$\;v_i>0, v_j>0$　2$\;v_i=0, v_j=0$　3$\;X_i>0, X_j>0$　4$\;X_i=0, X_j=0$

$\fbox{エ}$ の選択肢：

1$\;n^2$　2$\;\cfrac{n^2}{2}$　3$\;\cfrac{n^2}{4}$　4$\;1$　5$\;\cfrac{1}{2}$　6$\;\cfrac{1}{4}$

$\fbox{オ}$ の選択肢：

1$\;n^2$　2$\;2n^2$　3$\;4n^2$　4$\;1$　5$\;4$

$\fbox{カ}$ の選択肢：

1$\;n^2$　2$\;\cfrac{n^2}{2}$　3$\;2n^2$　4$\;n^4$

解答形式

空欄 $\fbox{ア}$ 〜 $\fbox{カ}$ には，半角数字 1 - 6 のいずれかが当てはまります。$\fbox{ア}$ 〜 $\fbox{カ}$ に当てはまるものを改行区切りで入力してください。

$$
|{\sqrt{i^2}-\sqrt{2i^2}}||{\sqrt{i^2}+\sqrt{3i^2}}||{\sqrt{2i^2}-\sqrt{4i^2}}||{\sqrt{2i^2}+\sqrt{4i^2}}|\\を求めて下さい。
$$
$$
(1)24(2)36(3)42(4)54
$$

$$\int_0^{\frac{1}{3}}\pi(-\frac{1}{2}x+1)^2dx$$

$$
\int_{0}^{m}\sqrt{\sqrt{x}^{4}}dm\int_{0}^{n}\sqrt{\sqrt{y}^{4}}dn\\について、積分して下さい。
$$
$$
(1)\frac{1}{2}{m}^2{n}^2
(2)\frac{1}{3}{m}^2{n}^2
(3)\frac{1}{4}{m}^2{n}^2
(4)\frac{1}{5}{m}^2{n}^2
$$