数学の問題一覧
公開日時: 2026年1月2日18:12 / ジャンル: 数学 / カテゴリ: 算数 / 難易度: / ジャッジ形式: 自動ジャッジ
パズル 西暦問題 虫食算 2026年問題
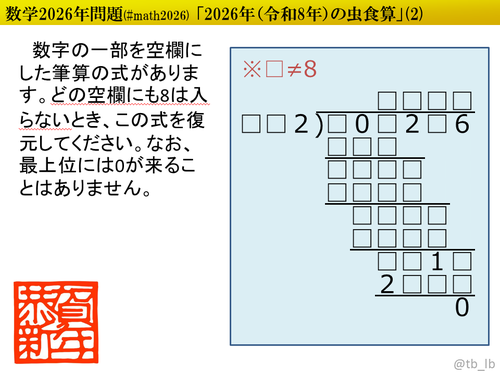
${}$ 西暦2025年問題第2弾です。第1弾に引き続き虫食算で、今回は割り算にしてみました。数学的手法(約数や倍数、偶奇性や剰余、不等式による絞り込み、などなど)を適宜用いることで面倒な場合分けや仮置きを軽減できるよう仕込んでいるのは変わりません。パズル的に解くのもよし、数学的にゴリゴリ解くのもよし、どうぞお好きなようにお楽しみください!
解答形式
${}$ 解答は2行目を「被除数÷除数」の形で入力してください。
(例) $2026 \div 102 = 19$ 余り $88$ → $\color{blue}{2026 \text{÷} 102}$
入力を一意に定めるための処置です。数字は半角で、「÷」の演算記号はTeX記法(\div)でも、絵文字や環境依存文字でもなく、全角記号の「÷」でお願いします。空白(スペース)も入れる必要はありません。
公開日時: 2026年1月1日18:45 / ジャンル: 数学 / カテゴリ: 算数 / 難易度: / ジャッジ形式: 自動ジャッジ
パズル 西暦問題 虫食算 2026年問題
${}$ 2026年、あけましておめでとうございます。本年もよろしくお願いいたします。
さて、新年数日は西暦である2026を織り込んだ数学やパズルの問題をお送りします。
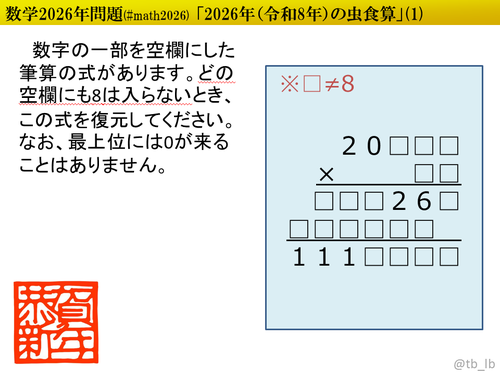
初日・2日目は虫食算です。虫食算というと確定マスから埋めていき、時には場合分けや仮置きを利用するのが定番の手法ですが、僕が作る虫食算は数学的手法(約数や倍数、偶奇性や剰余、不等式による絞り込み、などなど)を適宜用いることで面倒な場合分けや仮置きを軽減できるようにしています。とはいえ、解き方は自由です。お好きなようにパズルなひと時をお楽しみください。
解答形式
${}$ 解答は上2行を「被乗数×乗数」の形で入力してください。
(例) $2026 \times 101 = 204626$ → $\color{blue}{2026 \text{×} 101}$
入力を一意に定めるための処置です。数字は半角で、「×」の演算記号はTeX記法(\times)でも、絵文字や環境依存文字でもなく、全角記号の「×」でお願いします。空白(スペース)も入れる必要はありません。
公開日時: 2026年1月1日0:00 / ジャンル: 数学 / カテゴリ: 算数 / 難易度: / ジャッジ形式: 自動ジャッジ
競技数学 算数
問題文
ある神社ではおみくじを販売していて、おみくじの内容について次のようなことが分かっています。
・くじは2026本あり、それぞれに運勢が1つ書いてある。
・運勢は7種類あり、大吉、中吉、小吉、凶、大凶、吉、平である。
・(大吉の本数):(中吉の本数)=5:7
・(中吉の本数):(小吉の本数)=9:11
・(小吉の本数):(凶の本数)=7:4
・(凶の本数):(大凶の本数)=11:8
・(吉の本数):(平の本数)=5:2
平の本数を求めてください。
解答形式
答えの数字を半角数字で入力してください。
雑談
ここ3年ぐらい吉しか引いてないです。
(追記)今年も吉だったので4年連続です。
公開日時: 2025年7月22日9:17 / ジャンル: 数学 / カテゴリ: 算数 / 難易度: / ジャッジ形式: ジャッジなし
問題文
ある数は2の倍数であり、1を引くと3の倍数である。この数を、小さい順で10個答えよ
解答形式
数字を10個
公開日時: 2025年7月15日18:22 / ジャンル: 数学 / カテゴリ: 算数 / 難易度: / ジャッジ形式: 採点者ジャッジ
問題文
プロジェクト空間 $\mathbb{P}^2$ 内の射影多様体 $V = Z(x^3 + y^3 + z^3) \subset \mathbb{P}^2$ を考える。この多様体が非特異であることを示しなさい。
解答形式
証明してください。
公開日時: 2025年4月26日9:00 / ジャンル: 数学 / カテゴリ: 算数 / 難易度: / ジャッジ形式: 採点者ジャッジ
問題文
聖くんと光くんはトランプゲームを行うことにした.
なお$1$ から $13$ までの数字が書かれたトランプをそれぞれ四枚ずつ用いる.
ルールは以下の通り.
- 聖くんはトランプを $1$ 枚から$3$ 枚まで引くことができる.
- 光くんは幾つかの質問をして,聖くんが引いたトランプに書かれた数字を回答する.
光くん「書かれた数字の和を教えて」
聖くん「$31$ だよ」
光くん「うーん難しいな……なにかヒントくれない?」
聖くん「トランプに書かれた数字の積を求めたら、各位の和は $2$ になったよ」
光くんが引いたトランプの目として考えられるものを全て求めなさい。
解答形式
答えが$1,2,4$の場合は$(1,2,4)$と入力して下さい.(小さい順に)
公開日時: 2025年4月4日17:09 / ジャンル: 数学 / カテゴリ: 算数 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
以下の無限級数の値を求めてください。
$$ S = \sum_{n=1}^{\infty} \frac{1}{n^2 \binom{2n}{n}} $$
ここで、
$$
\begin{pmatrix} 2n \\ n \end{pmatrix}=\frac{(2n)!}{(n!)^2}
$$は中央二項係数です。
解答形式
$\frac{9^2}{5}$の場合は、9^2/5のように解答してください。
公開日時: 2025年3月26日16:37 / ジャンル: 数学 / カテゴリ: 算数 / 難易度: / ジャッジ形式: 自動ジャッジ
累乗
問題文
$327498^{789798}の1000000桁を求めよ。$
解答形式
半角英数字で解答してください。
公開日時: 2025年3月26日15:58 / ジャンル: 数学 / カテゴリ: 算数 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
56の10000乗を求めなさい。
解答形式
半角英数字で解答してください。(17709桁)