数学の問題一覧
公開日時: 2026年2月19日15:42 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
$\boxed{1}, \boxed{-1}, \boxed{1+i}, \boxed{1-i}$ の4枚のカードから無作為に1枚取り出して,書かれている数字を記録して,元に戻す操作を $n$ 回繰り返す。$k$ 回目に取り出したカードに書かれてる数を $X_k$ とする。
$\displaystyle P_n=\prod_{k=1}^{n} X_k$ が正の実数になる確率を $n$ を用いて表してください。
解答形式
$n$ が奇数のとき
$P_n=\dfrac 1a\left(b+\left(\dfrac dc\right)^{n-1}\right)$
$n$ が偶数のとき
$P_n=\displaystyle\dfrac 1e\left(f+\left(\dfrac hg\right)^{n-1}
+\left(\dfrac ji\right)^{\frac{ln}{k}-m}\right)$
と表せるので,$a+b+c+d+e+f+g+h+i+j+k+l+m$ の値を入力してください。
※$n$ が紛らわしいので注意
公開日時: 2026年2月18日13:30 / ジャンル: 数学 / カテゴリ: / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
下図の塗りつぶされた部分の面積を求めよ。
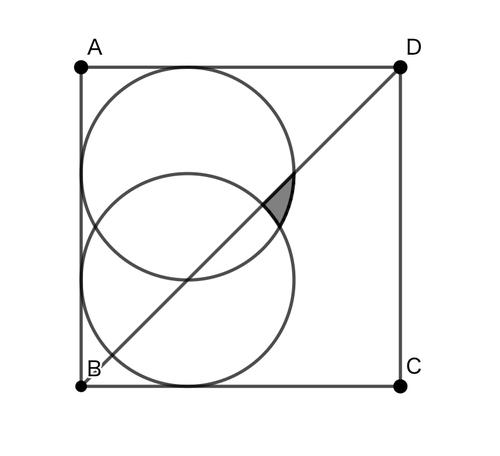
条件
・四角形$ABCD$は一辺の長さが$3$の正方形
・円はどちらも正方形の$2$辺に接していて、その半径は$1$
解答形式
答えは正整数$a,c$と平方因子を持たない正整数$b$および互いに素な正整数$d,e$を用いて$\dfrac{π}{a}+\dfrac{\sqrt{b}}{c}-\dfrac{d}{e}$と表されるので、$a+b+c+d+e$の値を半角数字で入力してください。
公開日時: 2026年2月17日4:37 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
$$\displaystyle \lim_{n\to\infty}\log_{e^{n}}\,{}_{2n}\mathrm{C}_{n}$$を求めてください。
解答形式
半角で数字のみ入力してください。
・答えが分数になる場合は分母と分子の和を答えてください。
(例: $\dfrac{1}{2}$ → $3$を入力する )
・答えに$\pi$を含む場合は$\pi=3$として答えてください。
(例: $2\pi$ → $6$を入力する,$\dfrac{\pi}{2}$ → $5$を入力する )
・答えに$\log$を含む場合は$a\log b$となる場合も$\log b^a$として真数のみ答えてください。
(例: $2\log 2$ → $4$を入力する )
・上記の例に当てはまらない場合は$0$と入力してください。($0$に収束する場合も$0$と入力します)
公開日時: 2026年2月12日20:43 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
三角形 累乗 ルート 整理
問題文
二等辺三角形ABCがあり、AB=AC=xcmである。また、頂角は150°である。下の式が二等辺三角形ABCの面積の値と等しくなった時、xの数値を求めなさい。(・は掛け算の×を表しています)
$$
\frac{x^4-10x^2+9}{(x+1)(x+3)(x-3)} + \sqrt{25+4\sqrt{6}} \cdot \sqrt{25-4\sqrt{6}} + \frac{(x+2)^3-(x-2)^3}{12x} + \frac{\sqrt{2}}{\sqrt{3}+\sqrt{1}} + \frac{\sqrt{2}}{\sqrt{5}+\sqrt{3}} + \frac{\sqrt{2}}{\sqrt{7}+\sqrt{5}} - \frac{\sqrt{14}}{\sqrt{2}} + 19
$$
解答形式
x=は必要ありません。数値のみを記入してください
(例) 810
公開日時: 2026年2月11日13:00 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
三角形ABCの
Pを線分AB上にABを2:3に内分するように、
Qを直線BC上にBCを1:2に外分するように、
Rを直線AC上に取ったところ、
P,Q,Rは一直線上にありました
この時、AR/CRの値を求めてください。
解答形式
解答する値は互いに素な自然数(a,b)を用いてa/bと表せるので、a+bの値を求めてください
公開日時: 2026年2月4日1:46 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
初等幾何
問題文
円に内接する四角形 $ABCD$ があり,$\angle ABC = 90^\circ$ をみたしている.$2$ 点 $A , C$ を通り直線 $AB$ に接するような円と線分 $BD$ の交点を $E$ とすると,$CD = CE$ が成立した.$BE = 7 , ED = 9$ であるとき,線分 $AB$ の長さの2乗を求めよ.
解答形式
半角数字で解答してください.
公開日時: 2026年2月2日17:29 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
$AB=44,AC=46$ をみたす三角形 $ABC$ があり, $AB,AC$ の中点を $M,N$ とする. 三角形 $ANB$ の外接円と三角形 $AMC$ の外接円の $A$ でない交点を $P$ とすると $P$ が線分 $BC$ 上に存在した.
このときの線分 $BC$ の長さを求めよ
解答形式
$BC^2$ は正の整数値になるので, その値を半角で解答してください
公開日時: 2026年2月2日8:54 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 採点者ジャッジ