金木犀の自作問題（2022/02/13）

Kinmokusei 自動ジャッジ 難易度: 数学 > 中学数学
2022年2月13日22:06 正解数: 7 / 解答数: 12 (正答率: 58.3%) ギブアップ数: 0
ツイートする
問題
解答一覧
全解答 自分の解答
質問(0) 解説

問題文

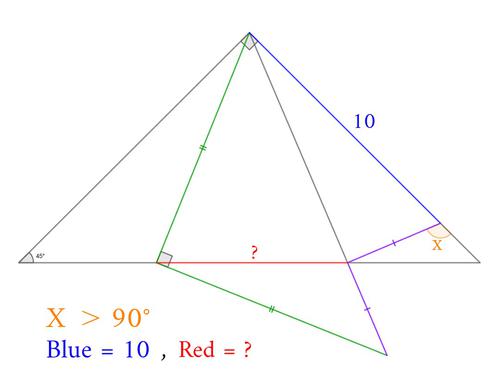
半円と直角三角形を組み合わせた以下の図について、青で示した線分と赤で示した線分の長さの比を求めてください。

解答形式

$\left(\dfrac{x}{y}\right)^2$ の値を半角数字で解答してください。

スポンサーリンク

解答提出

この問題は自動ジャッジの問題です。 解答形式が指定されていればそれにしたがって解答してください。

Discordでログイン Sign in with Google パスワードでログイン

ログインすると？ ログインすると、解答・ギブアップをする他に、問題を投稿したり、ランキングで競うことができます。

または

おすすめ問題

この問題を解いた人はこんな問題も解いています

求長問題8

Kinmokusei 自動ジャッジ 難易度:
4年前

8

問題文

2つの直角二等辺三角形が、それらの斜辺が交点をもつように配置されています。青い線分の長さが10、Xで示した角が鈍角のとき、赤い線分の長さを求めてください。
ただし、同じ色で示した線分の長さはそれぞれ等しいです。

解答形式

（赤い線分の長さ）$=[ア]\sqrt{[イ]}$ となります。
ただし、$[ア],[イ]$にはそれぞれ自然数が入ります。$[ア]+[イ]$を解答してください。また、$[イ]$に入る自然数はできるだけ小さくしてください。
例: （赤い線分の長さ）$=3\sqrt5$ なら、$3+5\rightarrow8$と解答

3年前

13

問題文

図の条件の下で、水色で示した三角形の面積を求めてください。

解答形式

求める面積 $x$ は互いに素な正整数 $a,b$ を用いて $x=\dfrac{a}{b}$ と表せるので、$a+b$ を解答してください。

3年前

8

問題文

半円弧を組み合わせた以下の図について、緑で示した部分の面積を求めてください。
大きい半円の直径は6、小さい半円弧の直径は3であり、大きい半円の弧は灰色の点によって6等分されています。

解答形式

解答は $\dfrac{a}{b}\pi$ となるので、$a+b$ を解答してください。
ただし、$a,b$ は互いに素な正整数です。

3年前

7

問題文

図の条件の下で、青で示した角の大きさを求めてください。

解答形式

$x=a$ 度 です。$a$ に当てはまる、0以上180未満の値を半角数字で解答してください。

求長問題21

Kinmokusei 自動ジャッジ 難易度:
4年前

6

問題文

扇形の内部に図のように線を引きました。赤い線分の長さが$2\sqrt 5$のとき、青い線分の長さを求めてください。

解答形式

半角数字で解答してください。

求長問題24

Kinmokusei 自動ジャッジ 難易度:
4年前

10

問題文

半円と、その中心を通る円が図のように配置されています。赤、青で示した弧の長さがそれぞれ3, 4のとき、緑で示した弧の長さを求めてください。

解答形式

半角数字で解答してください。

求長問題22

Kinmokusei 自動ジャッジ 難易度:
4年前

10

問題文

長方形に内接する半円があります。青い三角形の面積が9のとき、赤い線分の長さを求めてください。

解答形式

半角数字で解答してください。

求面積問題30

Kinmokusei 自動ジャッジ 難易度:
3年前

11

問題文

正三角形・長方形・半円を組み合わせた以下の図形について、図中緑の線分の長さが6のとき、図形全体の面積を求めてください。

解答形式

半角数字で解答してください。

求面積問題17

Kinmokusei 自動ジャッジ 難易度:
4年前

8

問題文

2つの合同な長方形を図のように配置しました。赤い三角形の面積が10のとき、青い凹四角形の面積を求めてください。

解答形式

半角数字で解答してください。

求角問題16

Kinmokusei 自動ジャッジ 難易度:
3年前

9

問題文

正六角形内に、図のように円を配置しました。青で示した角の大きさを求めてください。

解答形式

$\angle x=a°$ です。$a$ に当てはまる0以上180未満の数値を半角で回答してください。

求面積問題28

Kinmokusei 自動ジャッジ 難易度:
3年前

10

問題文

正方形に図のように線を引きました。外側の正方形の一辺が10のとき、青で示した部分の面積を求めてください。

解答形式

解答は自然数 $a,b$ によって $\dfrac{a}{b}$ と表せるので $a+b$ の値を半角数字で解答してください。

求角問題13

Kinmokusei 自動ジャッジ 難易度:
3年前

9

問題文

正方形・正三角形・円を組み合わせた以下の図について、$x$で示した角の大きさを求めてください。

解答形式

半角数字で、0以上180未満の整数を解答してください。
「度」や「°」などの単位を付けないよう注意してください。