この問題はコンテスト「ハッピーハロウィン!!!」の問題です。
解説
正$10$角形の面積を$S$とすると、
$S=10×\dfrac{1}{2}・31^2sin(\dfrac{360°}{10})$
$=5・31^2sin36°$
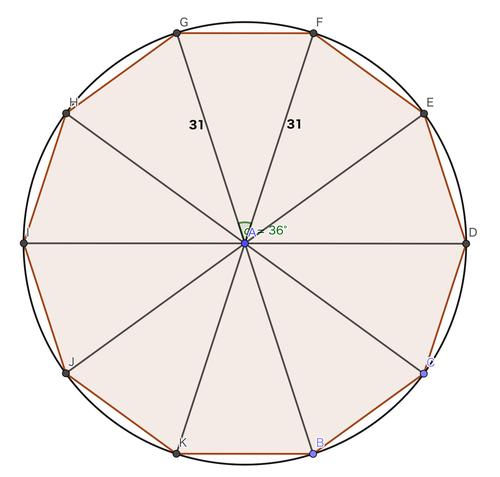
$θ=36°$とおき、$sinθ$の値を求める。
$5θ=180°$より$3θ=180°-2θ$
両辺の$sin$をとって$sin3θ=sin(180°-2θ)$
ゆえに$sin3θ=sin2θ$
$3sinθ-4sin^3θ=2sinθcosθ$
$sinθ≠0$であるから、$3-4sin^2θ=2cosθ$
変形して$4cos^2θ-2cosθ-1=0$
$cosθ>0$より$cosθ=\dfrac{1+\sqrt{5}}{4}$
したがって$sinθ=\dfrac{\sqrt{10-2\sqrt{5}}}{4}$
よって$S= \dfrac{5・31^2\sqrt{10-2\sqrt{5}}}{4}$
特に解答すべき値は$4824$。
おすすめ問題
この問題を解いた人はこんな問題も解いています