数学の問題一覧
公開日時: 2026年1月10日21:49 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
整数問題 西暦問題 2026年問題
${}$ 西暦2026年問題第10弾です。今年の最終回を迎えました。最終回はどこから手を付けていいのか迷ういそうな問題を用意しています。とはいえ、タネに気づけばサクッと解けるように仕込んであります。じっくりと腰を据えてお楽しみください。
解答形式
${}$ 解答は求める$x$の値を小さい順に2行に分けて半角で入力してください。「$x=$」の記載は不要です。
(例)$x=$110, 2026 → 《1行目》$\color{blue}{110}$、《2行目》$\color{blue}{2026}$
公開日時: 2026年1月8日21:52 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
整数問題 西暦問題 2026年問題
${}$ 西暦2026年問題第8弾です。$2026$を$2^{26}$とする強引な西暦問題となりました。ついでに書くと、どこかに類題がありそうで、その点でも恐れています。皆さんはそんな僕の恐れなど気にせずにお楽しみください。
解答形式
${}$ 解答は1行目に$p_3$の値を、2行目に$p_4$の値を、それぞれ半角で入力してください。「$p_3=$」「$p_4=$」といった記載は不要です。
(例)$p_3=$108、$p_4=$2026 → 《1行目》$\color{blue}{108}$、《2行目》$\color{blue}{2026}$
公開日時: 2026年1月7日23:24 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
整数問題 西暦問題 2026年問題
${}$ 西暦2026年問題第7弾です。見た目も実際もがっつり整数問題です。ひととき整数と戯れてみてください。
なお、$2026$より大きい整数の素数判定が待ち受けています。適宜、素数表(たとえば https://en.wikipedia.org/wiki/List_of_prime_numbers )を利用するなり、Wolfram|Alpha( https://www.wolframalpha.com )を利用するなりしてください。
解答形式
${}$ 解答は求める値をそのまま半角で入力してください。
(例)107 → $\color{blue}{107}$
求められているのは平方数と素数に挟まれた数であることに注意してください。
公開日時: 2026年1月4日22:09 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
整数問題 西暦問題 2026年問題
${}$ 西暦2026年問題第4弾です。見た目こそ覆面算風味の整数問題ですが、はたして……? 桁数の多い計算が待っていますので、適宜電卓をお使いください。
解答形式
${}$ 解答は1行目に$x$の値を、2行目に$d$の値を、それぞれ半角で入力してください。「$x=$」「$d=$」といった記載は不要です。
(例)$x=$104、$d=$4 → 《1行目》$\color{blue}{104}$、《2行目》$\color{blue}{4}$
公開日時: 2025年11月9日12:27 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
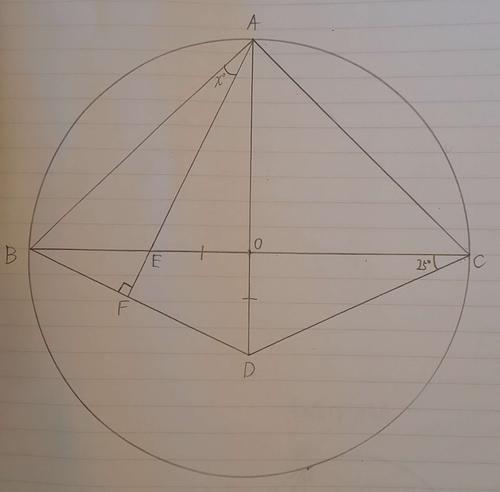
円Oの直径BCを斜辺とし、円周上に点Aを取った三角形ABCと、線分AOを少し延長したところに点Dを取った三角形BCDがある。そこに、∠Aから辺BDに垂直な線分を書き、その交点を点Fとした。EO=DO,∠OCD=25°のとき、∠BAFは何度ですか。
解答形式
例)〇〇°





