正方形と円の接線

kusu394 自動ジャッジ 難易度: 数学 > 競技数学
2024年6月17日0:53 正解数: 4 / 解答数: 5 (正答率: 80%) ギブアップ数: 1
ツイートする
問題
解答一覧
全解答 自分の解答
質問(1)

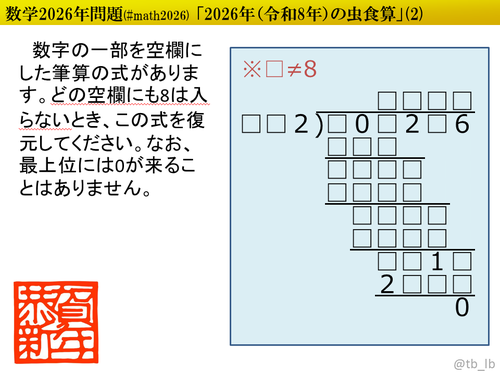
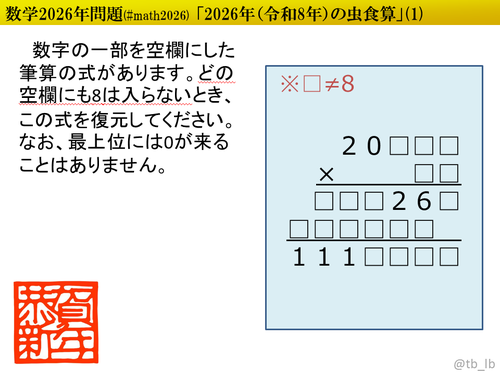
問題文

正方形 $ABCD$ の辺 $BC$ 上に点 $E$ をとると，
$$BE=7,\ \ \ \ CE=5$$が成り立ちます．$E$ を中心とした半径 $7$ の円を $O$ とし，正方形 $ABCD$ の内部かつ円 $O$ の周上の点 $F$ をとると直線 $DF$ は円 $O$ の接線となりました．このとき，線分 $CF$ の長さは正整数 $a,b$ と素数 $c$ を用いて $\displaystyle{\frac{a+\sqrt{b}}{c}}$ と書けるので $a+b+c$ の値を解答してください．

解答形式

答えは正の整数値となるので, その整数値を半角で入力してください．

追記
答えひらがなな訳ありませんでした、失礼しました

ヒント1

$\sqrt{b}$ は $d\sqrt{e}$ を $\sqrt{d^2e} $ の形で書き直した値，すなわち $b=d^2e$ の値を解答することになります．

ヒント2

うまく共円を見つけてください

スポンサーリンク

解答提出

この問題は自動ジャッジの問題です。 解答形式が指定されていればそれにしたがって解答してください。

Discordでログイン Sign in with Google パスワードでログイン

ログインすると？ ログインすると、解答・ギブアップをする他に、問題を投稿したり、ランキングで競うことができます。

または

おすすめ問題

この問題を解いた人はこんな問題も解いています

中線と垂線

kusu394 自動ジャッジ 難易度:
8月前

5

問題文

$\angle ABC $ と $\angle BCA$ が鋭角であるような $\triangle ABC$ について，辺 $BC$ の中点を $M$ とします．また，$M$ から辺 $AB,AC$ におろした垂線の足をそれぞれ $P, Q$ とすると、線分 $AM, BQ, CP$ が一点で交わります．

$$ AB = 12, \ \ BC= 20 $$

のとき，$\triangle ABC$ の面積の二乗としてありうる値の総和を解答してください。

解答形式

答えは正の整数値となるので, その整数値を半角で入力してください．

幾何作問練習3改

Lamenta 自動ジャッジ 難易度:
8月前

4

問題文

$AB>AC$なる鋭角三角形$ABC$において, $C$から$AB $に下ろした垂線の足を$D$, $BC$の中点を$M$, $AM$と$CD$の交点を$E$とし, 円$BDM$と$CD$の交点のうち$D$ではない方を$F$, 円$CDM$と$AM$の交点のうち$M$ではない方を$G$とします. $CD=32$, $DM=20$, $EF=5$であるとき, $FG$の長さの$2$乗を解答してください.

解答形式

半角数字で入力してください.

内接円の半径

nepia_nepinepi 自動ジャッジ 難易度:
3月前

4

問題文

半径$3$の円に内接する六角形$ABCDEF$ は以下の2つの条件をみたします:

四角形$ABDE, BCEF,CDFA$は長方形
周長が$15$

このとき,三角形$ACE$の内接円の$\textbf{半径}$を求めてください。

解答形式

答は非負整数$a,b$を用いて$\frac{a}{b}$と表されるので$a+b$の値を半角数字で答えてください。

幾何作問練習2

Lamenta 自動ジャッジ 難易度:
10月前

16

問題文

$AB=AC$なる鋭角二等辺三角形$ABC$において$AB$,$BC$の中点をそれぞれ$M$,$N$とし、$MC$の垂直二等分線と$AN$の交点を$P$とします。$\triangle ABC$の面積は$15$であり、$AP:PN=4:1$であるとき、$BC^4$を解答してください。

解答形式

半角数字で解答してください。

文化祭算数問題 3

sta_kun 自動ジャッジ 難易度:
7月前

13

問題文

四角形 $ABCD$ について，線分 $BD$ 上に点 $E$ を取ると，$AE=BD$ で，角 $EAD=$ 角 $AED=$ 角 $EBC=$ 角 $BCE=40°$ が成り立ちました．このとき角 $BDC$ は何度ですか？

解答形式

半角数字で解答してください．

2のべき乗と三角形

kusu394 自動ジャッジ 難易度:
6月前

5

問題文

$a + b + c = 999$ かつ $a \le b \le c$ を満たす正整数の組 $(a, b, c)$ であって，
$2^a, 2^b, 2^c$ が非退化な三角形の三辺の長さとなるものは何通りありますか．

解答形式

答えは正の整数値となるので，その整数値を半角で入力してください．

16月前

4

問題文

三角形 $ABC$ において，$A,B,C$ から対辺に下ろした垂線の足を $D,E,F$ とし，三角形 $ABC$ の垂心を $H$ としたところ，$DE=9,DF=8,DH=7$ となりました．
このとき，$AH$ の長さは互いに素な正の整数 $a,b$ を用いて $\dfrac{a}{b}$ と表されるので，$a+b$ の値を解答してください．

解答形式

半角数字で解答してください．

図形

ammonitenh3 自動ジャッジ 難易度:
6月前

6

問題文

三角形ABCとその辺AB上にある点Dと辺CA上にある点Eが次の二つの条件を満たしている．（ただし、点D,Eは点Aとは一致しない）
　（Ⅰ）AB=13,BC=14,CA=15
　（Ⅱ）4点B,C,E,Dは共円
　このとき、「点Aを通りDEに垂直な直線」と、線分BCの交点をFとする．
　BFの長さを求めよ．

解答形式

例）この答えは、互いに素な自然数$a$,$b$を用いて$\frac{a}{b}$と書けるので、$a$+$b$の値を答えてください．

10月前

6

問題文

正三角形 $ ABC$ の辺 $AB,BC,CA$ 上にそれぞれ点 $P,Q,R$ があり，
$$PQ=3,\ \ \ \ QR=5,\ \ \ \ RP=7,\ \ \ \ AB=9$$ を満たしています．このとき，線分 $AQ$ の長さは互いに素な整数 $a,b$ を用いて $\displaystyle \frac{a}{b}$ と書けるので $a+b$ の値を解答してください．

解答形式

答えは正の整数値となるので, その整数値を半角で入力してください．

大きい数の位の値

noname 自動ジャッジ 難易度:
6月前

7

問題文

$1998^{2024}$の下$2$桁を求めよ。

解答形式

1行目に半角整数で入力してください。

7月前

16

問題文

$\log_227$の整数部分を答えよ

文化祭算数問題 2

sta_kun 自動ジャッジ 難易度:
7月前

12

問題文

四角形 $ABCD$ について，角 $DBC=20°$，角 $BDC=90°$，角 $ADB=40°$，$AD:BC=1:2$ が成り立ちました．このとき角 $ABD$ は何度ですか？

解答形式

半角数字で解答して下さい．