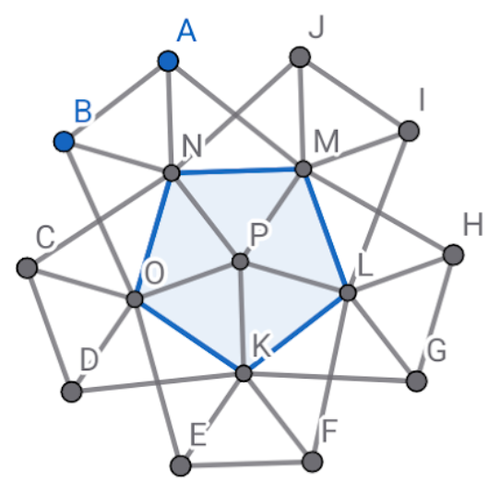
この問題はコンテスト「組合せしか出題しません」の問題です。
全 15 件
| 回答日時 | 問題 | 解答者 | 結果 | |
|---|---|---|---|---|
| 2026年2月23日8:18 | 問題15 |
|
不正解
|
|
| 2026年1月26日22:03 | 問題15 |
|
不正解
|
|
| 2026年1月15日20:56 | 問題15 |
|
不正解
|
|
| 2025年12月27日14:18 | 問題15 |
|
不正解
|
|
| 2025年12月27日14:16 | 問題15 |
|
不正解
|
|
| 2025年12月24日22:54 | 問題15 |
|
不正解
|
|
| 2025年12月21日17:43 | 問題15 |
|
不正解
|
|
| 2025年12月20日16:46 | 問題15 |
|
不正解
|
|
| 2025年12月17日0:47 | 問題15 |
|
不正解
|
|
| 2025年12月17日0:47 | 問題15 |
|
不正解
|
|
| 2025年12月17日0:31 | 問題15 |
|
不正解
|
|
| 2025年12月14日18:11 | 問題15 |
|
不正解
|
|
| 2025年12月13日16:49 | 問題15 |
|
不正解
|
|
| 2025年12月13日16:48 | 問題15 |
|
不正解
|
|
| 2025年12月13日16:43 | 問題15 |
|
不正解
|
おすすめ問題
この問題を解いた人はこんな問題も解いています