求長問題28

問題文

図の条件の下で、線分 $OO'$ の長さを求めてください。

解答形式

$OO'^2$ は正整数になるので、その値を半角数字で解答してください。

問題文

図の条件の下で，青で示した線分の長さを求めてください．

※頂角 $30°$ の合同な二等辺三角形

解答形式

$x^2$ の値を半角数字で解答してください．

問題文

半円と直角三角形を組み合わせた以下の図について、青で示した線分と赤で示した線分の長さの比を求めてください。

解答形式

$\left(\dfrac{x}{y}\right)^2$ の値を半角数字で解答してください。

問題文

2つの正六角形を組み合わせた、図のような七角形があります。青で示した部分の面積が49、赤で示した部分の面積が28のとき、緑で示した三角形の面積を求めてください。

解答形式

半角数字で解答してください。

問題文

図の条件の下で、水色で示した三角形の面積を求めてください。

解答形式

求める面積 $x$ は互いに素な正整数 $a,b$ を用いて $x=\dfrac{a}{b}$ と表せるので、$a+b$ を解答してください。

問題文

2つの合同な長方形を図のように配置しました。赤い三角形の面積が10のとき、青い凹四角形の面積を求めてください。

解答形式

半角数字で解答してください。

（2022/08/14 0:12追記）

問題文に誤りがあったため、修正しました。

問題文

頂角が $30$ 度または $90$ 度である二等辺三角形を図のように配置しました。このとき、ピンクで示した角の大きさは何度ですか？

解答形式

ピンクの角 $=x$ 度です。$x$ に当てはまる $0$ 以上 $180$ 未満の値を半角数字で解答してください。

問題文

図の条件の下で、緑で示した三角形の面積を求めてください。
なお、点 $I$ は直角三角形の内心です。

解答形式

解答は互いに素な正整数 $a,b$ を用いて $\dfrac{a}{b}$ と表されるので、$a+b$ の値を半角数字で解答してください。

問題文

図の条件の下で、青で示した線分の長さ $x$ を求めてください。
なお、緑で示した２つの角の大きさは等しく、ピンクで示した点は三角形の重心です。

解答形式

半角数字で解答してください。

問題文

一辺が $8$ である正三角形 $ABC$ の内接円と $AB,BC,CA$ との接点を $K,L,M$ とします。$\triangle ABC$ の外接円上の点 $P$ について、$PK^2+PL^2+PM^2$ の値を求めてください。

解答形式

半角数字で解答してください。

問題文

長方形に内接する半円があります。青い三角形の面積が9のとき、赤い線分の長さを求めてください。

解答形式

半角数字で解答してください。

問題文

2つの直角二等辺三角形が、それらの斜辺が交点をもつように配置されています。青い線分の長さが10、Xで示した角が鈍角のとき、赤い線分の長さを求めてください。
ただし、同じ色で示した線分の長さはそれぞれ等しいです。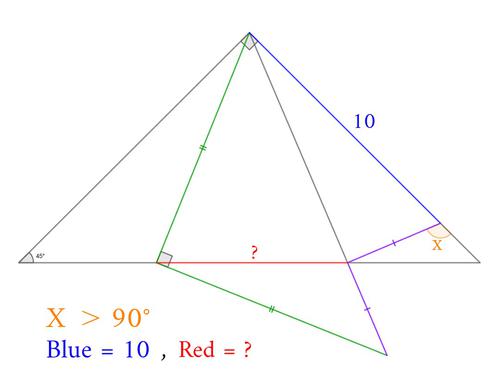

解答形式

（赤い線分の長さ）$=[ア]\sqrt{[イ]}$ となります。
ただし、$[ア],[イ]$にはそれぞれ自然数が入ります。$[ア]+[イ]$を解答してください。また、$[イ]$に入る自然数はできるだけ小さくしてください。
例: （赤い線分の長さ）$=3\sqrt5$ なら、$3+5\rightarrow8$と解答