全問題一覧
問題文
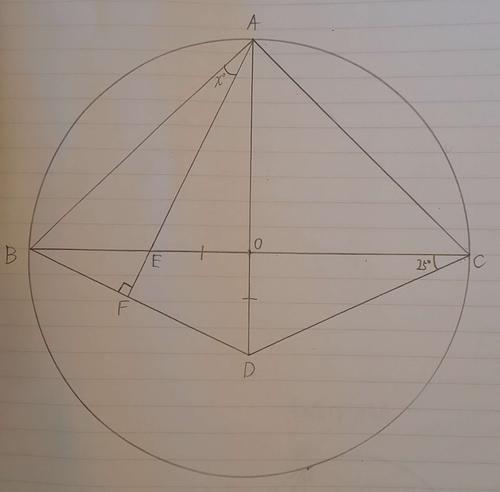
円Oの直径BCを斜辺とし、円周上に点Aを取った三角形ABCと、線分AOを少し延長したところに点Dを取った三角形BCDがある。そこに、∠Aから辺BDに垂直な線分を書き、その交点を点Fとした。EO=DO,∠OCD=25°のとき、∠BAFは何度ですか。
解答形式
例)〇〇°
問題文
x≧0, y≧0, x|2x+y|+y|x-2y|=2を満たすとき、x+2yのとりうる値の最大値と最小値を求めよ。また、そのときのx,yの値も求めよ。
解答形式
一行目に最小値、二行目に最大値を書いてください。
x+2yはx=○○, y=□□のとき最小値△
x=●●, y=■■のとき最大値▲
のように答える。
答えにルートが出る場合は、有理化はして答えること。また、”,”の後には空白はありません。