全問題一覧
公開日時: 2025年9月29日18:35 / ジャンル: 数学 / カテゴリ: / 難易度: / ジャッジ形式: 採点者ジャッジ
問題文
素数を無限に生成する2次多項式は存在するか。
公開日時: 2025年9月28日21:00 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
$n$ を $3$ 以上の奇数とします.いま,円に内接する凸 $n$ 角形 $P_1P_2\dots P_n$ があり,$k=1,2,\dots,n$ について角 $P_k$ の大きさを ${a_k}^{\circ}$ としたところ,
$$\sum_{k=1}^{\frac{n-1}{2}}a_{2k}=7777$$
が成立しました.このとき,度数法での角 $P_1P_2P_n$ の大きさとして考えられる値の総和を解答してください.
解答形式
答えは非負整数値となるので,それを半角で解答してください.
公開日時: 2025年9月28日21:00 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
ある正の実数 $k$ があり,$x$ についての $4$ 次多項式 $f(x)$ を
$$f(x)=x^4+4kx^3+3kx^2+2kx+k$$
と定めます.方程式 $f(x)=0$ は相異なる $4$ 個の複素数解を持ったのでそれらを $\alpha,\beta,\gamma,\delta$ とし,さらに $x$ についての $4$ 次多項式 $g(x)$ を,$4$ 次の項の係数が $1$ であり,かつ方程式 $g(x)=0$ が $4$ 個の複素数解 $\dfrac{1}{\alpha},\dfrac{1}{\beta},\dfrac{1}{\gamma},\dfrac{1}{\delta}$ を持つように定めます.
$g(6)=2025$ であるとき,$k$ の値を求めてください.
解答形式
答えは互いに素な正整数 $a,b$ を用いて $\dfrac{a}{b}$ と表されるので,$a+b$ の値を解答してください.
公開日時: 2025年9月28日21:00 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
$26$ 種類あるアルファベットの大文字からなる文字列に対し,次のようにして整数を対応付けます.
- $k$ 文字の文字列を考える.$1\leq i\leq k$ なる整数 $i$ について $i$ 文字目が $a_i$ 番目のアルファベットの大文字であるとき,$a_1,a_2,\dots,a_k$ を続けて書く.
例えば,文字列 $CAT$ は,$C$ が $3$ 番目,$A$ が $1$ 番目,$T$ が $20$ 番目のアルファベットであるから $3120$ となります.このように,ある文字列に対応付けられる整数は一意に定まります.
いま,ある文字列に対応付く整数が $12012311821$ となりました.元の文字列として考えられるものはいくつありますか?
解答形式
答えは非負整数値となるので,それを半角で入力してください.
公開日時: 2025年9月28日21:00 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
$1000$ の正の約数の集合を $D$ とします.また,$999$ 次方程式
$$x^{999}+x^{998}+\dots+x+1=0$$
の $999$ 個の解を $x=x_1,x_2,\dots,x_{999}$ とします.このとき,
$$\sum_{d\in D}^{}\sum_{s=1}^{999} x_s^d$$
の値を求めてください.
解答形式
答えは非負整数値となるので,それを半角で解答してください.
公開日時: 2025年9月25日21:00 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
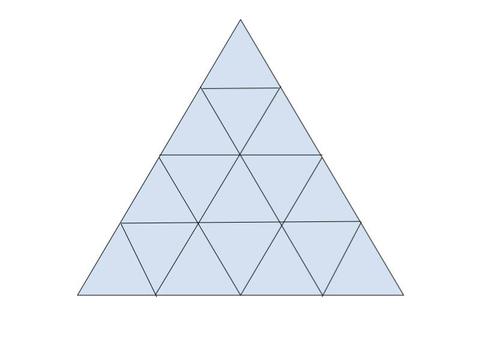
一辺の長さが $4$ の正三角形を、以下のように一辺の長さが $1$ の小正三角形 $16$ 個に分割します。
東くんがこの小正三角形それぞれに $0,1,2$ のいずれか一つを書き込むと、辺を共有して隣り合う $2$ つの小正三角形に書かれた数の差(の絶対値)はすべて $1$ でした。
このように東くんが書き込む方法は何通りありますか?ただし裏返しや回転によって一致する書き込み方も区別します。
解答形式
半角数字で解答してください
公開日時: 2025年9月25日21:00 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
複素数$\alpha,\beta,\gamma$が
$$\begin{cases}
\alpha+\beta+\gamma=9\\
\alpha^2+\beta^2+\gamma^2=25\\
\alpha^3+\beta^3+\gamma^3=2025
\end{cases}$$
を満たしています。このとき、$f(x)=0$ が $\alpha,\beta,\gamma $を解に持ち、かつ最高次係数が $1$ であるような $3$ 次関数 $f(x)$ が一意に存在するので、$❘f(2)❘$ を求めてください。
解答形式
解答は正の整数値になるので、その値を解答してください