数学の問題一覧
問題文
問題の数値設定に不備があったため、数値設定を変更します。申し訳ありません。(三角形 $DEH$ の面積を $9$ から $3$ に変更しました。)
鋭角三角形 $ABC$ の垂心を $H$, 外心を $O$ とします. また, 直線 $BH$ と線分 $AC$ の交点を $D$, 直線 $CH$ と線分 $AB$ の交点を $E$ とします. そして, 線分 $DE$ の中点を $N$, 直線 $HN$ と直線 $AO$ の交点を $X$ とします. このとき, $A, X, O$ はこの順に並び, $AX = 3, XO = 5$ が成立しました. また, 三角形 $DEH$ の面積が $3$ であったとき, 三角形 $ABC$ の面積を求めてください.
解答形式
答えは, 正整数 $a, b$ を用いて $\sqrt{a} + b$ と表されるので, $a+b$ の値を半角数字で解答してください.
問題文
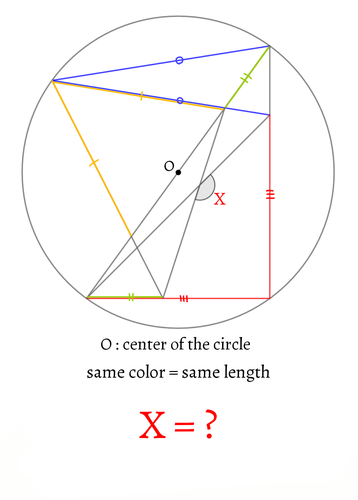
同じ色の線分は同じ長さです。
∠Xの大きさを求めてください。
青と黄、赤と黄緑の線分が重なって一部見づらくなっています。m(__)m
解答形式
度数法で、0~360の数字を半角で入力してください。
例:∠X=30° → 30
「度」や"°"をつけずに回答してください。
問題文
$k$を$0$以上の実数, $e$を自然対数の底とする。数列$a_n$を
$$a_n=\frac{n!e^n}{n^{n+k}}$$
と定める。任意の自然数$n$に対して, $a_{n+1} < a_n$が成り立つような最小の$k$を求めよ。
解答形式
整数または既約分数で答えてください。
問題文
$$
\sum_{k=1}^{10} {}_{10}{\mathrm{C}}_{k}\cdot9^k\cdot k
$$
解答形式
半角数字で入力してください。
問題文
鋭角三角形 $ABC$ の垂心を $H$,外心を $O$ とし,$A$ から $BC$ に下ろした垂線の足を $D$ とします.
$OH=3,AH:HD=7:2$ であり,$\triangle{ABC}$ の外接円半径が $5$ であるとき,${OD}^2$ の値は互いに素な正の整数 $a,b$ を用いて $\dfrac{a}{b}$ と表せるので,$a+b$ の値を解答してください.
解答形式
半角数字で解答してください.
問題文
以下の[条件]を満たす $3$ 桁の正の整数(つまり,$100$ 以上 $999$ 以下の正の整数)の組 $(A,B)$ すべてに対し,$A+B$ の値の総和を解答してください.
[条件] $A^2$ の下 $3$ 桁は $B$ であり,$B^2$ の下 $3$ 桁は $A$ である.
解答形式
半角数字で解答してください.
問題文
半径が $1,2,3,4,5$ の同心円に半径 $5$ の円の直径を $1$ 本付け加えて出来る図形を一筆書きで描く方法は何通りあるかを求めてください.
ただし,同じ道でも向きが異なる一筆書きは異なるものとして数えるものとします.
解答形式
半角数字で解答してください.
問題文
聖くんと光くんはトランプゲームを行うことにした.
なお,$1$ から $13$ までの数字が書かれたトランプをそれぞれ四枚ずつ用いる.
ルールは以下の通り.
- 聖くんはトランプを $1$ 枚から$3$ 枚まで引くことができる.
- 光くんは幾つかの質問をして,聖くんが引いたトランプに書かれた数字を回答する.
光くん「書かれた数字の和を教えて」
聖くん「$31$ だよ」
光くん「うーん難しいな……なにかヒントくれない?」
聖くん「トランプに書かれた数字の積を求めたら、各位の和は $2$ になったよ」
光くんが引いたトランプの目として考えられるものを全て求めなさい。
解答形式
答えが1,2,4の場合は(1,2,4)と入力して下さい.(小さい順に)
問題文
今年でSKG学院の学園祭は第$66$回を迎えます.また今年度は $2025$ 年です.
さて、$0,2,5$ のみを用いた数式の内,答えが $66$ となるようなものを一つ求めてください.
但し,演算子($+, -, \times$ など)は自由に用いて良いものとします.
一例:
$\left( (2 \times 0 \times 2 \times 5!) + (2 \times 0 \times 2 \times 5!) \right) \times \left( 2^2 + 0^2 + 2^2 + 5^2 \right) = (1+1) \times 33 = 66$
解答形式
式と答えを省略無しで入力して下さい.また,上の例とは違うものをお願いします.
問題文
長方形の4頂点と、ある1点を結びました。青い部分の面積の合計が10のとき、赤い三角形の面積を求めてください。
※半円は問題に関係ありません

解答形式
半角数字で解答してください。