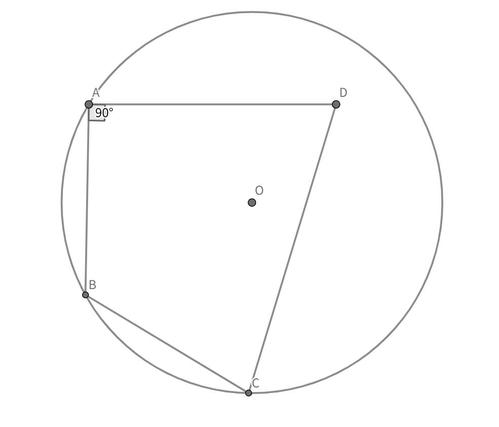
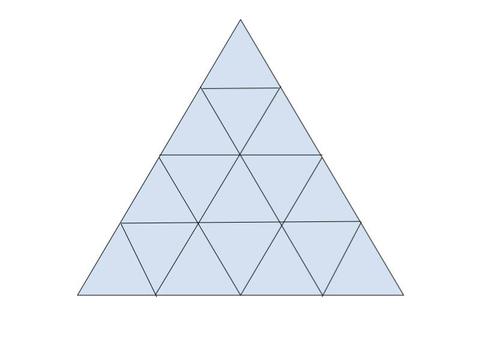
この問題はコンテスト「EMO (East Mathematics Olympiad)」の問題です。
全 27 件
| 回答日時 | 問題 | 解答者 | 結果 | |
|---|---|---|---|---|
| 2026年1月21日16:39 | 問題6 |
|
正解
|
|
| 2026年1月21日16:39 | 問題6 |
|
不正解
|
|
| 2025年9月26日21:26 | 問題6 |
|
正解
|
|
| 2025年9月26日17:31 | 問題6 | ゲスト |
正解
|
|
| 2025年9月26日15:29 | 問題6 |
|
正解
|
|
| 2025年9月25日22:21 | 問題6 |
|
不正解
|
|
| 2025年9月25日22:10 | 問題6 |
|
正解
|
|
| 2025年9月25日22:06 | 問題6 |
|
正解
|
|
| 2025年9月25日22:02 | 問題6 |
|
不正解
|
|
| 2025年9月25日22:00 | 問題6 |
|
不正解
|
|
| 2025年9月25日21:59 | 問題6 |
|
正解
|
|
| 2025年9月25日21:53 | 問題6 |
|
不正解
|
|
| 2025年9月25日21:52 | 問題6 |
|
正解
|
|
| 2025年9月25日21:51 | 問題6 |
|
正解
|
|
| 2025年9月25日21:41 | 問題6 |
|
正解
|
|
| 2025年9月25日21:40 | 問題6 |
|
正解
|
|
| 2025年9月25日21:31 | 問題6 |
|
正解
|
|
| 2025年9月25日21:30 | 問題6 |
|
不正解
|
|
| 2025年9月25日21:27 | 問題6 |
|
正解
|
|
| 2025年9月25日21:22 | 問題6 |
|
正解
|
|
| 2025年9月25日21:19 | 問題6 |
|
正解
|
|
| 2025年9月25日21:18 | 問題6 |
|
正解
|
|
| 2025年9月25日21:17 | 問題6 |
|
正解
|
|
| 2025年9月25日21:14 | 問題6 |
|
正解
|
|
| 2025年9月25日21:13 | 問題6 |
|
正解
|
おすすめ問題
この問題を解いた人はこんな問題も解いています