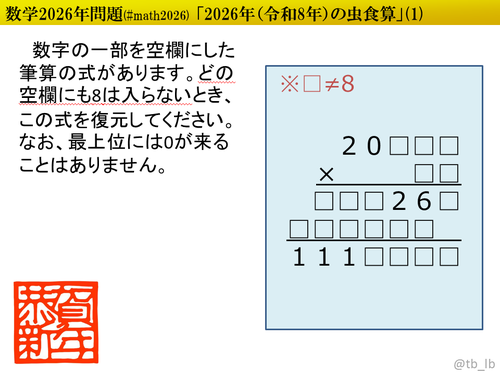
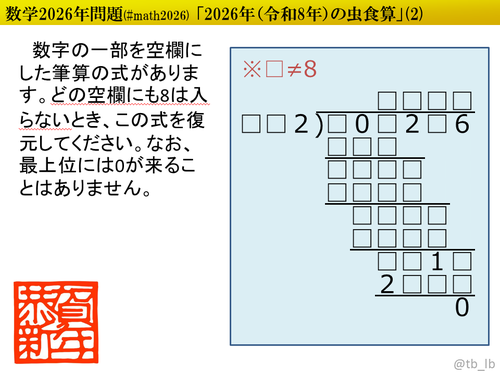
数列に現れる2026
2026年1月3日21:33
正解数: 5 /
解答数: 7
(正答率: 71.4%)
ギブアップ不可
${}$ 西暦2026年問題第3弾は規則性の問題でお送りします。あることに気づけば機械的な計算で答えが求まります。規則性の妙をお楽しみください。
解答形式
${}$ 解答は$n$の値を半角でそのまま入力してください。「$n=$」の記載は不要です。
(例)$n=103$ → $\color{blue}{103}$
なお、この条件を満たす$n$が存在しない場合には、$\color{blue}{-1}$と入力してください。
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています