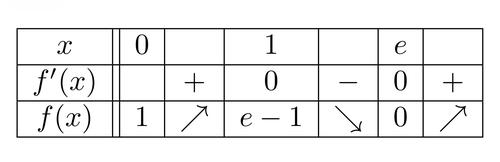問題文
次の問いに当てはまるx値を求めよ
この式はx/3になる
$$ \frac{2027^{2027} - 2027}{2027^{2026} - 1} + \left( \frac{2026^{2} + 2026}{2027} - 2026 \right)^{2027}$$
解答形式
x=は必要ありません。xに当てはまる数値のみ解答すれば良いです。
ヒント1
必要なのは根性と自信のみ!
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています