数学の問題一覧
公開日時: 2023年1月22日22:41 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
初等幾何 長さ

【補助線主体の図形問題 #086】
今週の図形問題です。今回は円弧と垂線を組み合わせてみました。円弧と垂線が組み合わさったときに生じる性質をお楽しみください。補助線が活躍するのはいつも通りですよ!
解答形式
${\def\cm{\thinspace \mathrm{cm}}}$ 解答は小数第3位を四捨五入して、小数第2位までを単位なしで入力してください。
(例) $12\cm$ → $\color{blue}{12.00}$ $10\sqrt{2}\cm$ → $\color{blue}{14.14}$ $\dfrac{1+\sqrt{5}}{2} \cm$ → $\color{blue}{1.62}$
入力を一意に定めるための処置です。
たとえば答えに無理数を含む場合、$\sqrt{2}=1.41$や$\pi=3.14$などでは必要な桁が足りない場合があるのでご注意ください。
近似値を求める際には、関数電卓やグーグルの電卓機能、Wolfram|Alpha https://www.wolframalpha.com などのご利用をお勧めします。
公開日時: 2025年3月26日16:37 / ジャンル: 数学 / カテゴリ: 算数 / 難易度: / ジャッジ形式: 自動ジャッジ
累乗
問題文
$327498^{789798}の1000000桁を求めよ。$
解答形式
半角英数字で解答してください。
公開日時: 2022年6月26日1:57 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
図の条件の下で、緑の線分の長さ $x$ を求めてください。

解答形式
$x^2$ の値を半角数字で解答してください。
公開日時: 2025年4月1日22:00 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
鋭角三三三角形 $ABCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC$ において,その外心を $O$,垂心を $H$,内接円を $\omega$ としたとき,$O,H$ はともに $\omega$ 上にあり,$\omega$ の半径は $1$ であった.
この条件下で線分 $OH$ の長さとしてありうる値の総積を $xxxxxxxxxx$ とする.$xxxxxxxxxx$ の最小多項式を $P$ として,$|P()|$ の値を解答せよ.ただし,$xxxxxxxxxx$ が最小多項式をもつことが保証される.
解答形式
半角数字を用いて解答せよ.解答すべき値が $$ でないことは保証される.
公開日時: 2024年2月21日21:00 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
初等幾何
問題文
問題の数値設定に不備があったため、数値設定を変更します。申し訳ありません。(三角形 $DEH$ の面積を $9$ から $3$ に変更しました。)
鋭角三角形 $ABC$ の垂心を $H$, 外心を $O$ とします. また, 直線 $BH$ と線分 $AC$ の交点を $D$, 直線 $CH$ と線分 $AB$ の交点を $E$ とします. そして, 線分 $DE$ の中点を $N$, 直線 $HN$ と直線 $AO$ の交点を $X$ とします. このとき, $A, X, O$ はこの順に並び, $AX = 3, XO = 5$ が成立しました. また, 三角形 $DEH$ の面積が $3$ であったとき, 三角形 $ABC$ の面積を求めてください.
解答形式
答えは, 正整数 $a, b$ を用いて $\sqrt{a} + b$ と表されるので, $a+b$ の値を半角数字で解答してください.
公開日時: 2020年12月5日19:26 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
周の長さが30である長方形ABCDがあります。辺CD上に∠APB=90°となるような点Pをとれるとき、長方形ABCDの面積の最大値を求めてください。
解答形式
半角数字で解答してください。
公開日時: 2024年9月21日16:23 / ジャンル: 数学 / カテゴリ: 競技数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
$1$ 以上 $12$ 以下の整数からなる集合を $U$ とし,空でない $U$ の部分集合 $S, T$ を
$$S \cup T = U,S \cap T = \phi$$となるよう定めたところ,$S$ の元の和と $T$ の元の平方和が等しくなりました.このような集合の組 $(S, T)$ すべてに対する「$S$ の元の和」の総和を解答して下さい.
たとえば,
$$S = \{1, 2, ..., 9\},T = \{10, 11, 12\}$$であるなら,$S$ の元の和は $1 + 2 + \cdots + 9 = 45$ と計算され,$T$ の元の平方和は $10^2 + 11^2 + 12^2 = 365$ と計算されます.
解答形式
半角英数にし、答えとなる正整数値を入力し解答して下さい.
公開日時: 2023年12月15日17:33 / ジャンル: 数学 / カテゴリ: 高校数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
「オ」「タ」「チ」の $3$ 種類の文字で構成される長さ $n$ の文字列に対して,オオタチ度を,その文字列の中で連続する $4$ 文字が「オオタチ」となっているようなものの数と定義します.
たとえば「チタタオオタチオタチタオオオタチ」のオオタチ度は $2$ で,「チタオオチタオオチタオオ」のオオタチ度は $0$ です.
長さが $n$ で構成する文字が $3$ 種類のため,文字列としては $3^n$ 種類のものが考えられます.これらのオオタチ度の相加平均を $f(n)$ とします.
$f(n)$ が正整数になる最小の $n$ を解答してください.
解答形式
半角数字で解答してください.
公開日時: 2020年6月10日14:17 / ジャンル: 数学 / カテゴリ: 中学数学 / 難易度: / ジャッジ形式: 自動ジャッジ
問題文
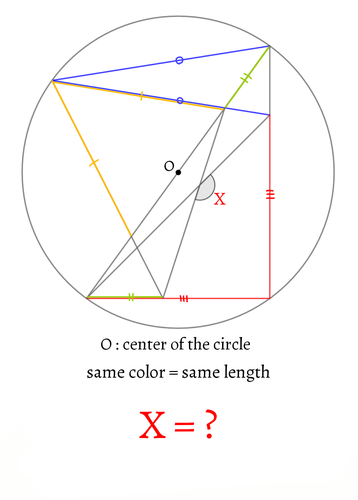
同じ色の線分は同じ長さです。
∠Xの大きさを求めてください。
青と黄、赤と黄緑の線分が重なって一部見づらくなっています。m(__)m
解答形式
度数法で、0~360の数字を半角で入力してください。
例:∠X=30° → 30
「度」や"°"をつけずに回答してください。