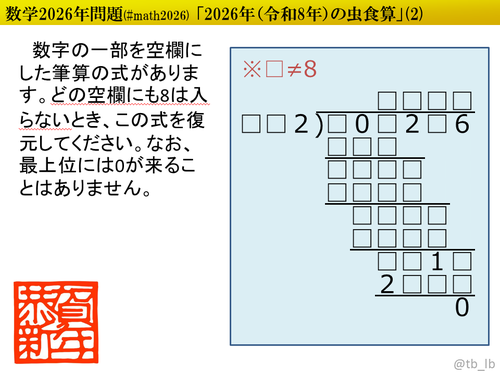
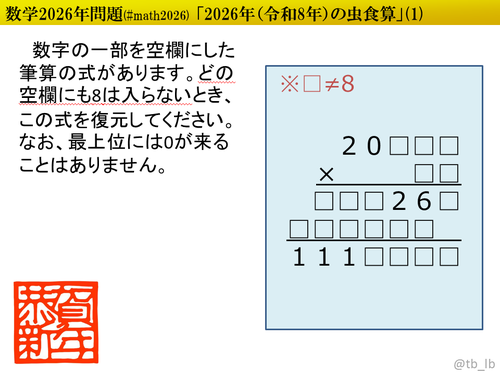
${}$ 西暦2026年問題第10弾です。今年の最終回を迎えました。最終回はどこから手を付けていいのか迷ういそうな問題を用意しています。とはいえ、タネに気づけばサクッと解けるように仕込んであります。じっくりと腰を据えてお楽しみください。
解答形式
${}$ 解答は求める$x$の値を小さい順に2行に分けて半角で入力してください。「$x=$」の記載は不要です。
(例)$x=$110, 2026 → 《1行目》$\color{blue}{110}$、《2行目》$\color{blue}{2026}$
${}$ 西暦2026年問題第9弾です。24時を回って、日付が変わってしまいました。僕の西暦問題では珍しく代数・解析分野からの出題となっています。さらにいうと、前回の問題と同じく$2026$を$2+2\sqrt{6}$と解釈する強引さを見せています。そんな珍しさと強引さを味わいながらお楽しみください。
解答形式
${}$ 解答は求める解の個数をそのまま半角で入力してください。
(例)109個 → $\color{blue}{109}$
なお、解が存在しない(不能)場合は$\color{blue}{0}$と、解が無数に存在する(不定)場合は$\color{blue}{\mathrm{inf}}$と入力してください。
${}$ 西暦2026年問題第8弾です。$2026$を$2^{26}$とする強引な西暦問題となりました。ついでに書くと、どこかに類題がありそうで、その点でも恐れています。皆さんはそんな僕の恐れなど気にせずにお楽しみください。
解答形式
${}$ 解答は1行目に$p_3$の値を、2行目に$p_4$の値を、それぞれ半角で入力してください。「$p_3=$」「$p_4=$」といった記載は不要です。
(例)$p_3=$108、$p_4=$2026 → 《1行目》$\color{blue}{108}$、《2行目》$\color{blue}{2026}$
${}$ 西暦2026年問題第7弾です。見た目も実際もがっつり整数問題です。ひととき整数と戯れてみてください。
なお、$2026$より大きい整数の素数判定が待ち受けています。適宜、素数表(たとえば https://en.wikipedia.org/wiki/List_of_prime_numbers )を利用するなり、Wolfram|Alpha( https://www.wolframalpha.com )を利用するなりしてください。
解答形式
${}$ 解答は求める値をそのまま半角で入力してください。
(例)107 → $\color{blue}{107}$
求められているのは平方数と素数に挟まれた数であることに注意してください。
${}$ 西暦2025年問題第2弾です。第1弾に引き続き虫食算で、今回は割り算にしてみました。数学的手法(約数や倍数、偶奇性や剰余、不等式による絞り込み、などなど)を適宜用いることで面倒な場合分けや仮置きを軽減できるよう仕込んでいるのは変わりません。パズル的に解くのもよし、数学的にゴリゴリ解くのもよし、どうぞお好きなようにお楽しみください!
解答形式
${}$ 解答は2行目を「被除数÷除数」の形で入力してください。
(例) $2026 \div 102 = 19$ 余り $88$ → $\color{blue}{2026 \text{÷} 102}$
入力を一意に定めるための処置です。数字は半角で、「÷」の演算記号はTeX記法(\div)でも、絵文字や環境依存文字でもなく、全角記号の「÷」でお願いします。空白(スペース)も入れる必要はありません。
${}$ 2026年、あけましておめでとうございます。本年もよろしくお願いいたします。
さて、新年数日は西暦である2026を織り込んだ数学やパズルの問題をお送りします。
初日・2日目は虫食算です。虫食算というと確定マスから埋めていき、時には場合分けや仮置きを利用するのが定番の手法ですが、僕が作る虫食算は数学的手法(約数や倍数、偶奇性や剰余、不等式による絞り込み、などなど)を適宜用いることで面倒な場合分けや仮置きを軽減できるようにしています。とはいえ、解き方は自由です。お好きなようにパズルなひと時をお楽しみください。
解答形式
${}$ 解答は上2行を「被乗数×乗数」の形で入力してください。
(例) $2026 \times 101 = 204626$ → $\color{blue}{2026 \text{×} 101}$
入力を一意に定めるための処置です。数字は半角で、「×」の演算記号はTeX記法(\times)でも、絵文字や環境依存文字でもなく、全角記号の「×」でお願いします。空白(スペース)も入れる必要はありません。
${}$ 西暦2025年問題第2弾です。第1弾に引き続き虫食算で、今回は掛け算にしてみました。数学的手法(約数や倍数、偶奇性や剰余、不等式による絞り込み、などなど)を適宜用いることで面倒な場合分けや仮置きを軽減できるよう仕込んでいるのは変わりません。パズル的に解くのもよし、数学的にゴリゴリ解くのもよし、どうぞお好きなようにお楽しみください!
解答形式
${}$ 解答は上2行を「被乗数×乗数」の形で入力してください。
(例) $2025 \times 102 = 206550$ → $\color{blue}{2025 \text{×} 102}$
入力を一意に定めるための処置です。数字は半角で、「×」の演算記号はTeX記法(\times)でも、絵文字や環境依存文字でもなく、全角記号の「×」でお願いします。空白(スペース)も入れる必要はありません。
${}$ 2025年、あけましておめでとうございます。昨年は図形問題の投稿を長らくお休みしてしまいましたが、本年もよろしくお願いいたします。
さて、新年数日は西暦である2025を織り込んだ数学やパズルの問題をお送りします。
初日・2日目は虫食算です。虫食算というと確定マスから埋めていき、時には場合分けや仮置きを利用するのが定番の手法ですが、僕が作る虫食算は数学的手法(約数や倍数、偶奇性や剰余、不等式による絞り込み、などなど)を適宜用いることで面倒な場合分けや仮置きを軽減できるようにしています。とはいえ、解き方は自由です。お好きなようにパズルなひと時をお楽しみください。
解答形式
${}$ 解答は2行目を「被除数÷除数」の形で入力してください。
(例) $2025 \div 101 = 20$ 余り $5$ → $\color{blue}{2025 \text{÷} 101}$
入力を一意に定めるための処置です。数字は半角で、「÷」の演算記号はTeX記法(\div)でも、絵文字や環境依存文字でもなく、全角記号の「÷」でお願いします。空白(スペース)も入れる必要はありません。

【補助線主体の図形問題 #126】
今週の図形問題です。隙あらば暗算で処理できる程度の問題を好んで出題しているのですが、今回は暗算処理は厳しいかもしれません。紙&ペンをご用意の上、挑戦していただければと思います。
解答形式
${
\def\cm{\thinspace \mathrm{cm}}
}$ 解答は小数第3位を四捨五入して、小数第2位までを単位なしで入力してください。
(例) $12\cm$ → $\color{blue}{12.00}$ $10\sqrt{2}\cm$ → $\color{blue}{14.14}$ $\dfrac{1+\sqrt{5}}{2} \cm$ → $\color{blue}{1.62}$
入力を一意に定めるための処置です。
たとえば答えに無理数を含む場合、$\sqrt{2}=1.41$や$\pi=3.14$などでは必要な桁が足りない場合があるのでご注意ください。
近似値を求める際には、関数電卓やグーグルの電卓機能、Wolfram|Alpha https://www.wolframalpha.com などのご利用をお勧めします。