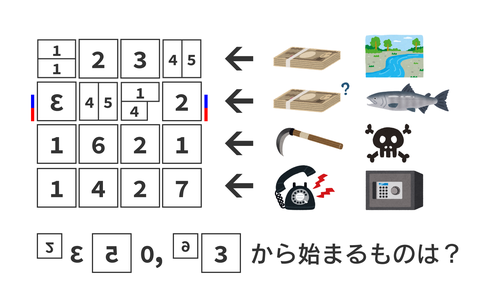
halphy
問題文
漸化式
$$
a_{n+3}=3a_{n+2}-4a_{n+1}+2a_n\quad (n=1,2,\cdots)
$$および
$$
a_1=1, \; a_2=0, \; a_3=0
$$を満たす数列 $\{a_n\}$ を考える。次の空欄 $\fbox{ア}$ 〜 $\fbox{フ}$ に当てはまる数字を答えなさい。
-
漸化式
$$
a_{n+3}=3a_{n+2}-4a_{n+1}+2a_n\quad (n=1,2,\cdots)
$$を満たす数列全体の集合を $V$ とする。数列 $a_n, b_n\in V$ および $c\in\mathbb{C}$ に対して,第 $n$ 項が $ca_n, a_n+b_n$ であるような数列をそれぞれ数列 $a_n$ の $c$ 倍,数列 $a_n, b_n$ の和と定義することにすると,この和とスカラー倍により $V$ は $\mathbb{C}$ 上のベクトル空間になる(確かめよ)。ここで,$V$ の元 $a_n$ は,$a_1, a_2, a_3$ を定めることで完全に決定できる。すなわち,写像 $\varphi: V \to \mathbb{C}^3$ を
$$
\varphi(a_n)=\begin{pmatrix} a_1 \\ a_2 \\ a_3\end{pmatrix}
$$で定めると,$\varphi$ は全単射である。しかも,$\varphi$ は線型写像だから,$\varphi$ はベクトル空間の同型になる。$V$ は $\fbox{ア}$ 次元である。また,$e_n^{(1)}, e_n^{(2)}, e_n^{(3)}\in V$ を
$$
\varphi(e_n^{(1)})=\begin{pmatrix} 1 \\ 0 \\ 0\end{pmatrix},\; \varphi(e_n^{(2)})=\begin{pmatrix} 0 \\ 1 \\ 0\end{pmatrix},\; \varphi(e_n^{(3)})=\begin{pmatrix} 0 \\ 0 \\ 1\end{pmatrix}
$$となるように定めると,$e_n^{(1)}, e_n^{(2)}, e_n^{(3)}$ は $V$ の基底になる。 -
$V$ 上の線型変換 $L: V\to V$ を次のように定義する。$a_n\in V$ に対して,$L(a_n)$ を第 $1, 2, 3$ 項がそれぞれ $a_2, a_3, a_4$ である数列とする($L$ が線型写像になることを確かめよ)。このとき,$L(a_n)$ の第 $n$ 項は $a_{n+\fbox{イ}}$ である。基底 $e_n^{(1)}, e_n^{(2)}, e_n^{(3)}$ のもとでの $L$ の表現行列 $L_A$ は
$$
L_A=\begin{pmatrix} \fbox{ウ} & \fbox{エ} & * \\ \fbox{オ} & \fbox{カ} & \fbox{キ} \\ \fbox{ク} & \fbox{ケコ} & \fbox{サ}\end{pmatrix}
$$である。 -
$L_A$ の固有値を $\lambda^{(1)}, \lambda^{(2)}, \lambda^{(3)}$ とする($\lambda^{(1)}\in\mathbb{R}, {\rm Im}(\lambda^{(2)})>0, {\rm Im}(\lambda^{(3)})<0$)。このとき
\begin{align}
\lambda^{(1)}&=\fbox{シ}\\
{\rm Re}(\lambda^{(2)})={\rm Re}(\lambda^{(3)})&=\fbox{ス}\\
{\rm Im}(\lambda^{(2)})=-{\rm Im}(\lambda^{(3)})&=\fbox{セ}
\end{align}である。 -
固有値 $\lambda^{(1)}, \lambda^{(2)}, \lambda^{(3)}$ に対応する固有ベクトルをそれぞれ $\alpha^{(1)}, \alpha^{(2)}, \alpha^{(3)}$ とする。固有ベクトルには定数倍の不定性があるが,$\alpha^{(j)}\;(j=1,2,3)$ の第 $1$ 成分が固有値 $\lambda^{(j)}$ に一致するようにとると
\begin{align}
\alpha^{(1)}=\begin{pmatrix} \lambda^{(1)} \\ \fbox{ソ} \\ * \end{pmatrix},\; \alpha^{(2)}=\begin{pmatrix} \lambda^{(2)} \\ \fbox{タ}\;i \\ * \end{pmatrix},\; \alpha^{(3)}=\begin{pmatrix} \lambda^{(3)} \\ * \\ \fbox{チツ}-\fbox{テ}\;i \end{pmatrix}
\end{align}である。 -
$\varphi(\beta_n^{(1)})=\alpha^{(1)}, \;\varphi(\beta_n^{(2)})=\alpha^{(2)}, \;\varphi(\beta_n^{(3)})=\alpha^{(3)}$ となる数列 $\beta_n^{(1)}, \beta_n^{(2)}, \beta_n^{(3)}\in V$ をとる。$\beta_n^{(1)}, \beta_n^{(2)}, \beta_n^{(3)}\in V$ は $V$ の基底をなすから,$V$ の任意の元 $a_n$ はこれらの線型結合で表すことができる。例えば,$a_n\in V$ が
$$
a_1=1, \; a_2=0, \; a_3=0
$$を満たすとき
$$
a_n=\fbox{ト}\;\beta_n^{(1)}-\frac{\beta_n^{(2)}-\beta_n^{(3)}}{\fbox{ナ}\; i}
$$が成り立つ。これを変形すると
$$
a_n=\fbox{ニ}-\left(\sqrt{\fbox{ヌ}}\;\right)^n\sin\left(\frac{n\pi}{\fbox{ネ}}\right)
$$となる。また,$a_1,\cdots, a_{100}$ のうち $a_n$ が最大となるのは $n=\fbox{ノハ}, \fbox{ヒフ}$ のときである。ただし $\fbox{ノハ} < \fbox{ヒフ}$ とする。
※この問題では,数列とは写像 $a: \mathbb{N} \to \mathbb{C}$ のことをいう。$n\in\mathbb{N}$ に対して,$a(n)$ のことを単に $a_n$ と表記する。また,記号の濫用であるが $a$ を $\{a_n\}, a_n$とも書く。
解答形式
空欄 $\fbox{ア}$ 〜 $\fbox{フ}$ には,半角数字 0 - 9 または記号 - のいずれかが当てはまります。$\fbox{ア}$ 〜 $\fbox{フ}$ に当てはまるものを改行区切りで入力してください。
問題文
$r$ を正の整数とする。$xyz$ 空間において,原点を中心とする半径 $\sqrt{r}$ の球面を $S_r$ で表すとき,次の問いに答えなさい。
- $S_r$ が格子点を含まないような最小の $r$ を求めなさい。
- $S_r$ が格子点を含まず,$r$ が $8$ の倍数であるような最小の $r$ を求めなさい。
※点 $(x,y,z)$ が格子点であるとは,$x,y,z$ がすべて整数であることをいう。
解答形式
改行区切りで,1行目に 1. の答えを,2行目に 2. の答えを入力してください。
問題文
ロシアの首都で人をハンバーガーショップに誘うとき何と言うでしょう?
*7/19 1:03 別解を追加しました。
※これはクソなぞなぞです。
問題文
(1) 正規表現
(((3|((2|5|8)(0|6|9)*3)|(((2|5|8)(0|6|9)*(1|4|7))|(6|9))(((0|6|9)*(2|5|8)(0|6|9)*(1|4|7))*(((0|6|9)*3?)|((0|6|9)*(2|5|8)(0|6|9)*3))))|(((1|4|7)|((2|5|8)(0|6|9)*(2|5|8))|((((2|5|8)(0|6|9)*(1|4|7))|(6|9))(((0|6|9)*(2|5|8)(0|6|9)*(1|4|7))*(((0|6|9)*(1|4|7))|((0|6|9)*(2|5|8)(0|6|9)*(2|5|8))))))((((0|6|9)*(1|4|7)(0|6|9)*(2|5|8))*(((0|6|9)*(2|5|8))|((0|6|9)*(1|4|7)(0|6|9)*(1|4|7))))(((0|6|9)*(2|5|8)(0|6|9)*(1|4|7))*(((0|6|9)*(1|4|7))|((0|6|9)*(2|5|8)(0|6|9)*(2|5|8)))))*((((0|6|9)*(1|4|7)(0|6|9)*(2|5|8))*(((0|6|9)*3)|((0|6|9)*(1|4|7)(0|6|9)*3)))|((((0|6|9)*(1|4|7)(0|6|9)*(2|5|8))*(((0|6|9)*(2|5|8))|((0|6|9)*(1|4|7)(0|6|9)*(1|4|7))))(((0|6|9)*(2|5|8)(0|6|9)*(1|4|7))*(((0|6|9)*3?)|((0|6|9)*(2|5|8)(0|6|9)*3))))))))|(.*3.*)
にマッチするような文字列を1つ答えなさい。
(2) 上の正規表現にマッチする文字列全体の集合から連想される人物名をひらがな8文字で答えなさい。
解答形式
改行区切りで入力してください。
問題文
$\mathbb{R}^3$上の単位球面
$$
S^2=\{(x,y,z)\in \mathbb{R}^3\mid x^2+y^2+z^2=1\}
$$
に対して,その開部分集合 $U=S^2\setminus \{(x,y,z)\in S^2 \mid x\geq 0, y=0\}$ を考える。また,$\mathbb{R}^2$ の部分集合を
$$
V=\{(\theta, \varphi)\in\mathbb{R}^2\mid -\pi/2 < \theta < \pi/2, \;0<\varphi <2\pi\}
$$
とおく。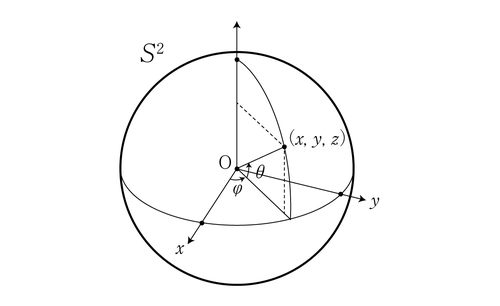
写像 $f:V\to U, g: V\to \mathbb{R}^2$ を次のように定める。
\begin{align}
f(\theta, \varphi)&=(\cos\theta\cos\varphi, \cos\theta\sin\varphi, \sin\theta)\\
g(\theta, \varphi)&=(\varphi \cos\alpha, \sin\alpha)
\end{align}ただし,$\alpha$ は,関係式
$$
\sin 2\alpha+2\alpha=\pi\sin\theta
$$
の唯一の解である。$g$ が単射であることは証明なしに用いてよい。
(1) $(\xi, \eta)=g(\theta, \varphi)$ とし,行列
$$
J(\theta, \varphi)=\begin{pmatrix} \cfrac{\partial\xi(\theta, \varphi)}{\partial \theta} & \cfrac{\partial\eta(\theta, \varphi)}{\partial \theta} \\ \cfrac{\partial\xi(\theta, \varphi)}{\partial \varphi} & \cfrac{\partial\eta(\theta, \varphi)}{\partial \varphi} \end{pmatrix}
$$を考える。このとき
$$
|{\rm det}\,J(\theta, \varphi)|=\fbox{ア}\cos\theta
$$
である。
(2) 領域 $g(f^{-1}(U))$ の面積は $\fbox{イ}$ である。
解答形式
空欄 $\fbox{ア}$, $\fbox{イ}$ には正の実数が当てはまる。これを $10$ 進小数に表し,小数第 $4$ 位以降を切り捨てたものを改行区切りで半角数字 0-9 およびピリオド . を用いて入力しなさい。例えば,$1.2345\cdots$ を当てはめるなら 1.234 と解答すること。
以下に,重複を除いた最初の $11$ 個のフィボナッチ数とそのチュクチ語訳がある。数字は小さい順,チュクチ語は辞書式順序で並んでいる。
$$
1,2,3,5,8,13,21,34,55,89,144
$$
ənnenmənɣətken ŋəroq paroɬmətɬəŋenŋer'amətɬəŋqɬekken ŋəraq paroɬŋəraqqɬekken ŋər'amətɬəŋen paroɬŋər'omətɬəŋenŋəroqŋireqŋireqqɬikkin kəɬɣənken paroɬqɬikkin ənnen paroɬqɬikkin mənɣətken ŋəraq paroɬ
問題文
- 数とチュクチ語との正しい対応関係を答えなさい。
- チュクチ語で書かれた次の等式を数字で書きなさい。
ŋəroq×ŋer'amətɬəŋen=qɬikkin ənnen paroɬ
- Aさんは、以下の等式の空欄 $\fbox{ X }$ に入る数詞が
ənnenmətɬəŋenだと予想したが、これは誤りであることが分かった。正しい答えをチュクチ語で書きなさい。mətɬəŋen× $\fbox{ X }$ =qɬikkin mənɣətken paroɬ
- チュクチ語で書きなさい: $15, 42, 60$
⚠︎ チュクチ語はチュクチ・カムチャツカ語族に属する。ロシア・チュクチ自治管区で約5,000人が使用している。
ɣ ɬ ŋ q ' は子音である。ə は母音である。
*7/19 9:30 ヒントを追加しました。
*7/20 0:06 ヒントを追加しました。
解答形式
- 問題 1 → 1行目〜11行目に答えを書きなさい。上から順に並んでいるチュクチ語の数詞に対応する数を,改行区切りで数字で書きなさい。
- 問題 2 → 12行目に答えを書きなさい。記入例:
1x1=1(掛け算記号にはxを用い,スペースを入れないこと) - 問題 3 → 13行目に答えを書きなさい。
- 問題 4 → 14行目〜16行目に改行区切りで答えを書きなさい。必要ならば半角スペースで分かち書きをすること。
問題文
$n$ を非負整数とする。縦の長さが $3$,横の長さが $2n$ の長方形をした部屋を,辺の長さが $1$ と $2$ の長方形の畳で敷き詰める方法の総数を $a_n$ とする。ただし,部屋を固定したとき,畳を回転または反転させて一致するような敷き詰め方は区別して数える。また,便宜上 $a_0=1$ と約束する。
例えば,縦の長さが $3$,横の長さが $2$ である部屋を畳で敷き詰める方法は
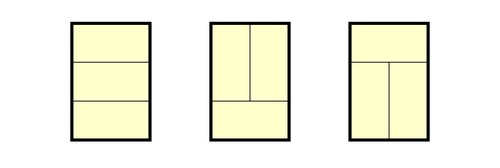 の $3$ 通りだから $a_1=3$ である。このとき
の $3$ 通りだから $a_1=3$ である。このとき
$$
a_n=\fbox{ア}\;a_{n-1}+\fbox{イ}\;\sum_{k=0}^{n-2}a_k\quad (n=2,3,\cdots)
$$が成り立つから
$$
a_4=\fbox{ウエオ}
$$である。また,上の漸化式を変形すると
$$
\lim_{n\to\infty}\frac{a_{n+1}}{a_n}=\fbox{カ}+\sqrt{\fbox{キ}}
$$が成り立つことが分かる。
解答形式
$\fbox{ア}$ 〜 $\fbox{キ}$ には,半角数字 0 - 9 のいずれかが当てはまります。$\fbox{ア}$ 〜 $\fbox{キ}$ に当てはまるものを,改行区切りで入力してください。
問題文
$n=0, 1,\cdots$ に対して
\begin{equation}
I_n=\int_0^1 \frac{x^n}{\sqrt{1-x^4}}dx
\end{equation}
と定める。この広義積分は収束することが知られている。
任意の $n=0,1,\cdots$ に対して
\begin{equation}
I_{n+\fbox{ア}}=\frac{n+\fbox{イ}}{n+\fbox{ウ}}I_n
\end{equation}が成り立つ(ただし $\fbox{ア}$ は $0$ でない)。これを利用すると
\begin{equation}
\prod_{n=1}^{\infty} \left[1-\frac{4}{(4n-1)^2}\right]=\frac{\fbox{エ}\;\pi^{\fbox{オ}}}{\alpha^{\fbox{カ}}}
\end{equation}が導かれる。ここで $\alpha$ は
\begin{equation}
\alpha=\int_0^{\infty} t^{-3/4}e^{-t}dt=\Gamma\left(\frac{1}{4}\right)
\end{equation}で定義される定数である(この広義積分は収束することが知られている)。
注意事項
以下の事実は証明なしに用いてよい。
- 実数 $x>0$ に対して,広義積分
\begin{equation}
\Gamma(x) := \int_0^{\infty} t^{x-1}e^{-t}\;dt
\end{equation}は収束する。 - 実数 $x>0$ に対して
\begin{equation}
\Gamma(x+1)=x\Gamma(x)
\end{equation}が成り立つ。 - 実数 $x, y>0$ に対して
\begin{equation}
\frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}=\int_0^1 t^{x-1}(1-t)^{y-1}\;dt
\end{equation}が成り立つ。ただし,右辺の広義積分は収束することが知られている。 - 実数 $0<x<1$ に対して
\begin{equation}
\Gamma(x)\Gamma(1-x)=\frac{\pi}{\sin\pi x}
\end{equation}が成り立つ(相反公式)。
解答形式
$\fbox{ア}$ 〜 $\fbox{カ}$ には,半角数字 0 - 9 のいずれかが当てはまります。$\fbox{ア}$ 〜 $\fbox{カ}$ に当てはまるものを,改行区切りで入力してください。
問題文
模造紙が嫌いな人が住んでいる地名ってな〜んだ?
解答形式
ひらがなで入力してください。
※これはクソなぞなぞです。
問題文
星野源と結婚してそうな人のレポートってな〜んだ?
*7/19 1:37, 1:41 別解を追加しました。
※これはクソなぞなぞです。
問題文
最近、重いものを運搬するときに頭に乗せて運ぶ人をよく見かけますね。
それでは、特に頭に本を乗せて運ぶ人のことをなんというでしょう?
※これはクソなぞなぞです。
問題文
$n\geq 2$ を自然数とする。$2$ 進数表記で
\begin{equation}
N=\underbrace{11\cdots 11}_n \underbrace{00\cdots 00} _ {n-1} {} _ {(2)}
\end{equation}と表される自然数 $N$ を考える。$n=13$ のとき,$N$ の正の約数の総和を求めなさい。
解答形式
$2$ 進数で答えなさい。
問題文
ポロロロ ポロロロ ポロロロ ポロロロ
ポロポロ ポロポロ ポロポロ ポロポロ
チャーン チャーン チャーンチャ
チャーン チャーン チャチャチャチャチャチャチャ
チャーン チャーン チャーンチャ
チャーン
(中略)
タタチャンチャンチャン タタチャンチャンチャン
チャーンチャンチャチャ タラララタラララタラララタラララ