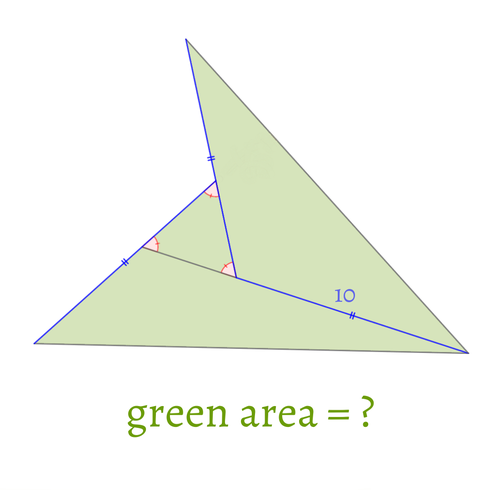
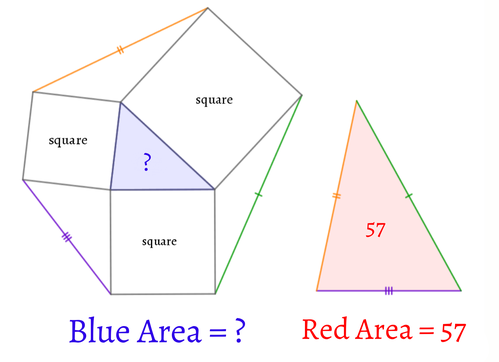
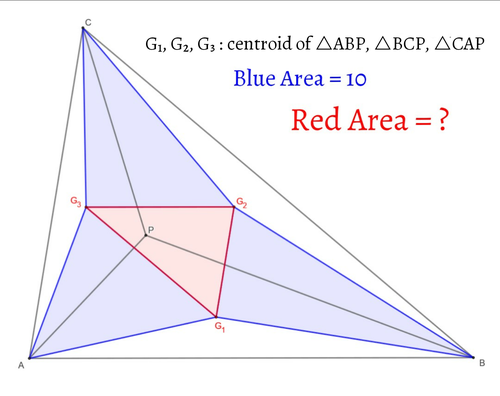
[B] Dots on the Ball
2020年8月15日18:00
正解数: 13 /
解答数: 25
(正答率: 52%)
ギブアップ不可
この問題はコンテスト「KOH Mathematical Contest #2」の問題です。
全 25 件
おすすめ問題
この問題を解いた人はこんな問題も解いています