問題文
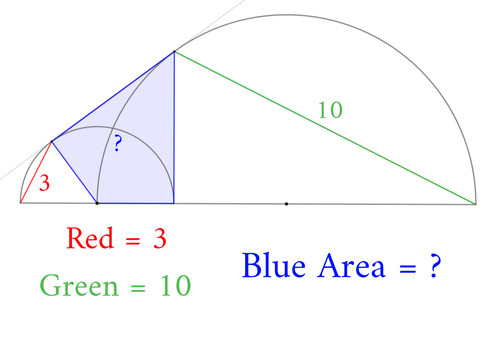
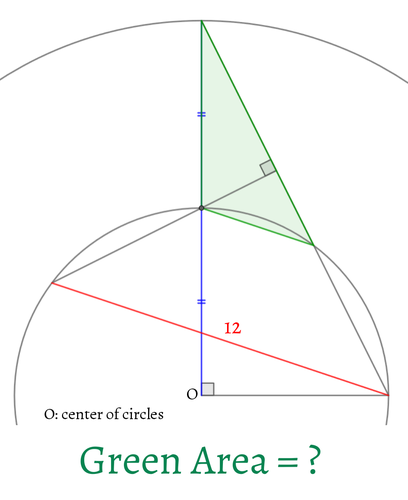
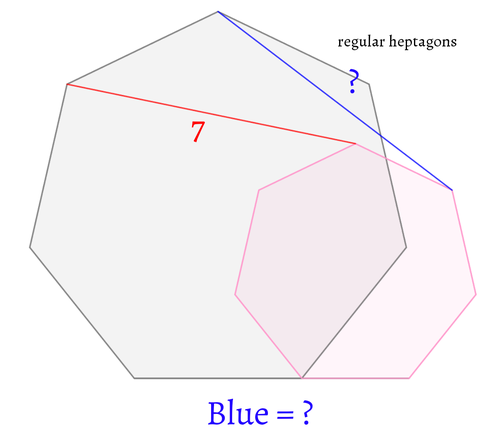
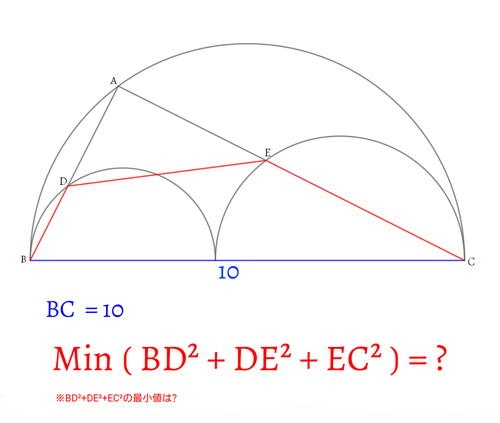
直径10の半円中に、直径の和が10となる2つの半円を図のように配置します。点Aを大半円の弧上にとり、線分AB,ACと小半円の交点をD,Eとします。
$BD^2+DE^2+EC^2$が最小となるようにしたとき、その最小値を求めてください。
解答形式
半角数字で解答してください。
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています