全問題一覧
${}$ 2026年、あけましておめでとうございます。本年もよろしくお願いいたします。
さて、新年数日は西暦である2026を織り込んだ数学やパズルの問題をお送りします。
初日・2日目は虫食算です。虫食算というと確定マスから埋めていき、時には場合分けや仮置きを利用するのが定番の手法ですが、僕が作る虫食算は数学的手法(約数や倍数、偶奇性や剰余、不等式による絞り込み、などなど)を適宜用いることで面倒な場合分けや仮置きを軽減できるようにしています。とはいえ、解き方は自由です。お好きなようにパズルなひと時をお楽しみください。
解答形式
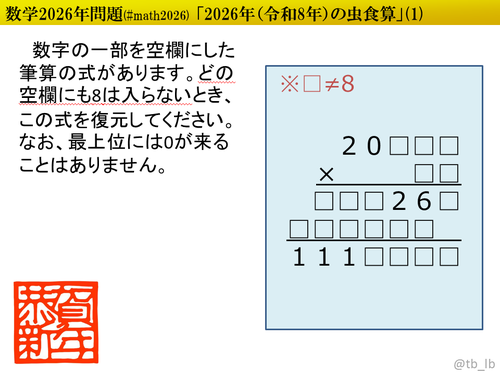
${}$ 解答は上2行を「被乗数×乗数」の形で入力してください。
(例) $2026 \times 101 = 204626$ → $\color{blue}{2026 \text{×} 101}$
入力を一意に定めるための処置です。数字は半角で、「×」の演算記号はTeX記法(\times)でも、絵文字や環境依存文字でもなく、全角記号の「×」でお願いします。空白(スペース)も入れる必要はありません。
問題文
$N=p^q-pq$とします。$N-1$が平方数、$p,q,\frac{N}{2},N+1,N+3$がいずれも素数になるような$N$としてありうる最小の値を求めてください。
解答形式
半角整数で答えてください。
問題文
ある神社ではおみくじを販売していて、おみくじの内容について次のようなことが分かっています。
・くじは2026本あり、それぞれに運勢が1つ書いてある。
・運勢は7種類あり、大吉、中吉、小吉、凶、大凶、吉、平である。
・(大吉の本数):(中吉の本数)=5:7
・(中吉の本数):(小吉の本数)=9:11
・(小吉の本数):(凶の本数)=7:4
・(凶の本数):(大凶の本数)=11:8
・(吉の本数):(平の本数)=5:2
平の本数を求めてください。
解答形式
答えの数字を半角数字で入力してください。
雑談
ここ3年ぐらい吉しか引いてないです。
(追記)今年も吉だったので4年連続です。
問題文
$2025^{2026}+2026^{2025}$ について以下の問いに答えよ。
$(1)$ $625$ で割った余りを求めよ。
$(2)$ 下 $4$ 桁の数を求めよ。
解答形式
答え二つを半角カンマ(,)で区切って答えてください。
例)123,456
追記:解答を修正しました。答えが合っているのに誤答判定された方は申し訳ございません。
問題文
正の整数 $n$ に対し,関数 $f_n(x)$ を
$$
f_n(x)=x\lfloor \dfrac{n}{x}\rfloor
$$
で定める.ただし,$x>0$ とする.
また,実数 $t$ に対し,$t$ 以下の最大の整数を $\lfloor t\rfloor$ で表す.
⑴ 方程式 $
f_n(x)=n$ が正の実数解を無限個もつことを示せ. また,$f_1(x)=1$ の正の実数解を,値が大きい順に
$$
a_1,a_2,a_3,\ldots
$$
とするとき,
$$
\lim_{m\to\infty}\sum_{k=m}^{2m} a_k
$$
を求めよ.
⑵ 座標平面における $y=f_n(x)$ のグラフのうち,$
\dfrac{1}{2}\le x\le 1
$ を満たす部分の長さの総和を $S_n$ とする.
このとき, $$ \lim_{n\to\infty}\dfrac{S_n}{n}
$$を求めよ.
解答形式
証明は入力せず、答えのみで良いです。
⑴の答えは1行目、⑵の答えは2行目に いずれも左詰めで入力してください。
入力例)
π 、√π、2e/3、log7 (自然対数)、(3+√2)π、5e√2、log10_2 (常用対数)
関数 $f:\mathbb{Z}^2\rightarrow \mathbb{Z}$ は以下を満たします.
- $f(0,0)=1$
- $n,m$ いずれかが $0$ 未満であるとき, $f(n,m)=0$.
- $(n,m)\neq(0,0)$ を満たす非負整数の組 $(n,m)$ に対して, 以下が成立.
$$
\begin{aligned}
&f(n,m)\\\\
&=f(n-1,m)+2f(n,m-1)\\\\
&+f(n-2,m)-f(n-1,m-1)-f(n,m-2)
\end{aligned}
$$
このとき$f(10000,10000)$ を 素数 $4999$ で割った余りを求めてください.