数学の問題一覧
問題文
ある正整数 $n$ が今年の数であるとは $n=a^b-(a-1)^b$ とあらわせるような正整数の組 $(a,b)$ が存在しない数であるとします.例えば$2026$は今年の数です.
このとき,$2026$以下の今年の数はいくつありますか.
$3$ 点 $A,B,C$ はこの順で一直線に並んでおり,$AC,AB,BC$ を直径とする円をそれぞれ $\omega_1,\omega_2,\omega_3$ とし,点 $B$ を通る直線と $\omega_1,\omega_2,\omega_3$ の交点を,$P,Q,B,R,S$ の順に並ぶように定めると,
$$AB<BC,\quad AB=\sqrt{390},\quad QB=18,\quad BR=24$$
が成り立ちました.このとき,互いに素な正整数 $m,n$ を用いて $PB:BS=m:n$ と表されるので,$m+n$ の値を解答してください.
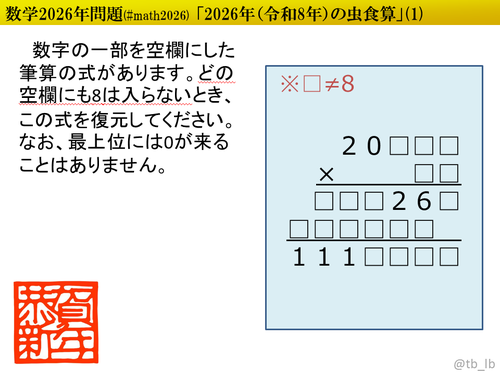
${}$ 西暦2025年問題第2弾です。第1弾に引き続き虫食算で、今回は割り算にしてみました。数学的手法(約数や倍数、偶奇性や剰余、不等式による絞り込み、などなど)を適宜用いることで面倒な場合分けや仮置きを軽減できるよう仕込んでいるのは変わりません。パズル的に解くのもよし、数学的にゴリゴリ解くのもよし、どうぞお好きなようにお楽しみください!
解答形式
${}$ 解答は2行目を「被除数÷除数」の形で入力してください。
(例) $2026 \div 102 = 19$ 余り $88$ → $\color{blue}{2026 \text{÷} 102}$
入力を一意に定めるための処置です。数字は半角で、「÷」の演算記号はTeX記法(\div)でも、絵文字や環境依存文字でもなく、全角記号の「÷」でお願いします。空白(スペース)も入れる必要はありません。
${}$ 2026年、あけましておめでとうございます。本年もよろしくお願いいたします。
さて、新年数日は西暦である2026を織り込んだ数学やパズルの問題をお送りします。
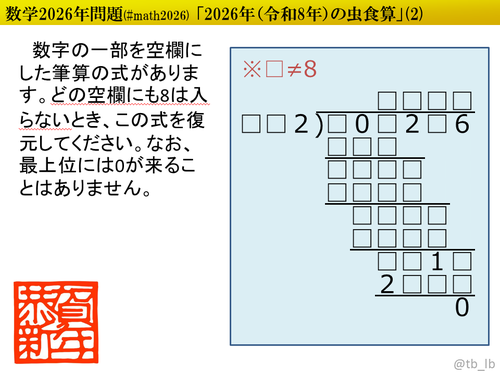
初日・2日目は虫食算です。虫食算というと確定マスから埋めていき、時には場合分けや仮置きを利用するのが定番の手法ですが、僕が作る虫食算は数学的手法(約数や倍数、偶奇性や剰余、不等式による絞り込み、などなど)を適宜用いることで面倒な場合分けや仮置きを軽減できるようにしています。とはいえ、解き方は自由です。お好きなようにパズルなひと時をお楽しみください。
解答形式
${}$ 解答は上2行を「被乗数×乗数」の形で入力してください。
(例) $2026 \times 101 = 204626$ → $\color{blue}{2026 \text{×} 101}$
入力を一意に定めるための処置です。数字は半角で、「×」の演算記号はTeX記法(\times)でも、絵文字や環境依存文字でもなく、全角記号の「×」でお願いします。空白(スペース)も入れる必要はありません。
問題文
$N=p^q-pq$とします。$N-1$が平方数、$p,q,\frac{N}{2},N+1,N+3$がいずれも素数になるような$N$としてありうる最小の値を求めてください。
解答形式
半角整数で答えてください。
問題文
ある神社ではおみくじを販売していて、おみくじの内容について次のようなことが分かっています。
・くじは2026本あり、それぞれに運勢が1つ書いてある。
・運勢は7種類あり、大吉、中吉、小吉、凶、大凶、吉、平である。
・(大吉の本数):(中吉の本数)=5:7
・(中吉の本数):(小吉の本数)=9:11
・(小吉の本数):(凶の本数)=7:4
・(凶の本数):(大凶の本数)=11:8
・(吉の本数):(平の本数)=5:2
平の本数を求めてください。
解答形式
答えの数字を半角数字で入力してください。
雑談
ここ3年ぐらい吉しか引いてないです。
(追記)今年も吉だったので4年連続です。