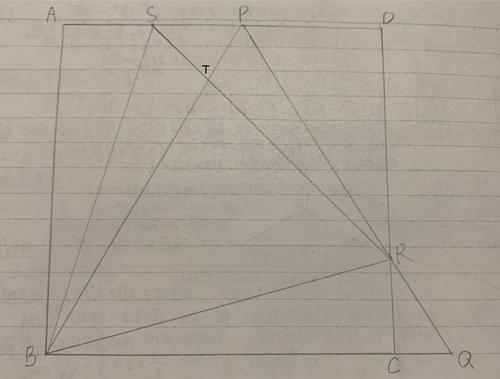
Isosceles triangle
2024年10月11日0:13
正解数: 3 /
解答数: 3
(正答率: 100%)
ギブアップ数: 0
全 3 件
| 回答日時 | 問題 | 解答者 | 結果 | |
|---|---|---|---|---|
| 2024年10月14日14:59 | Isosceles triangle |
|
正解
|
|
| 2024年10月12日12:35 | Isosceles triangle |
|
正解
|
|
| 2024年10月11日23:42 | Isosceles triangle |
|
正解
|
おすすめ問題
この問題を解いた人はこんな問題も解いています