問題文
問題文を3つの半円が図のように配置されています。赤い部分の面積が9、緑の部分の面積が5のとき、青い部分の面積を求めてください。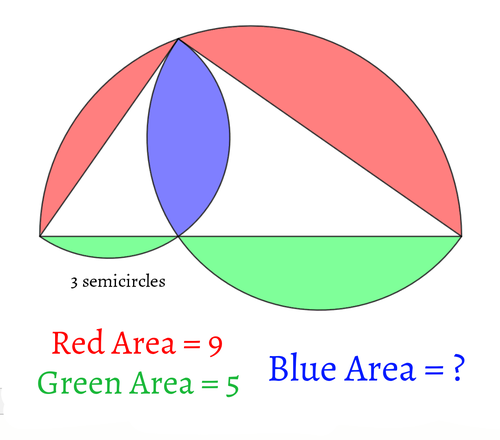
解答形式
半角数字で解答してください。
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています
問題文を3つの半円が図のように配置されています。赤い部分の面積が9、緑の部分の面積が5のとき、青い部分の面積を求めてください。
半角数字で解答してください。
この問題を解いた人はこんな問題も解いています