sEigEn sign
2025年8月27日3:27
正解数: 11 /
解答数: 15
(正答率: 73.3%)
ギブアップ数: 0
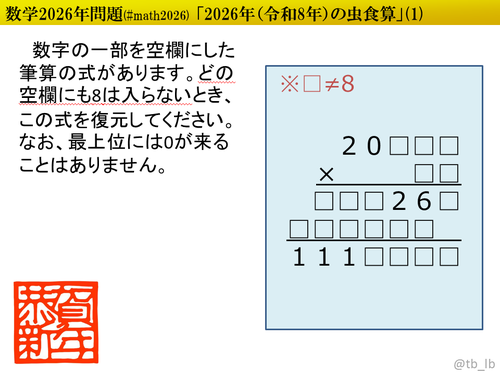
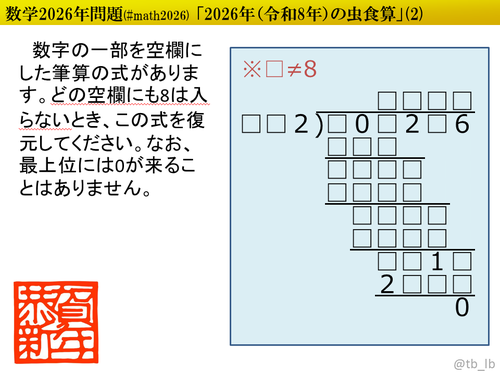
問題文
$\lim\limits_{n\to\infty} n\sin\frac{2π}{n} = mπ$ である。
$m$の値を求めよ。
解答形式
$m$は2つの実数$a,b$を使って $\frac{a}{b}$と表せる。
$m$を分母が有理化された既約分数の形にした時の$a+b$を解答すること。
ヒント1
円に内接する正多角形を考えましょう。
*ギブアップしても解説はありません。
ヒント2
正n角形を外接円の半径を辺にもつn個の三角形に分割して考えてみましょう。
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています