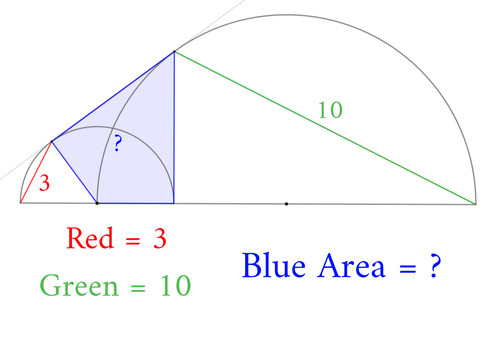
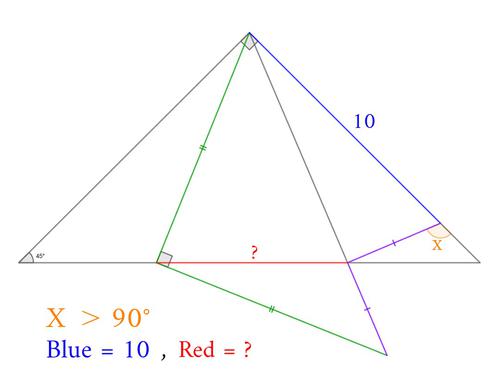
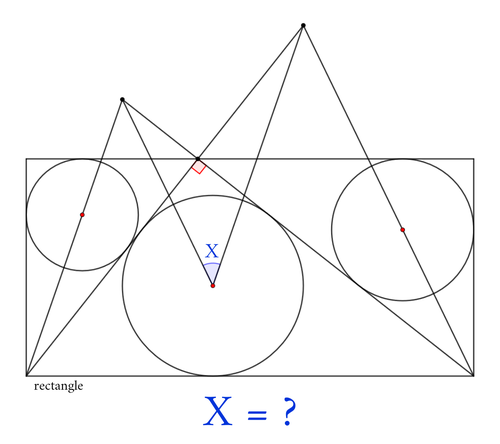
問題文
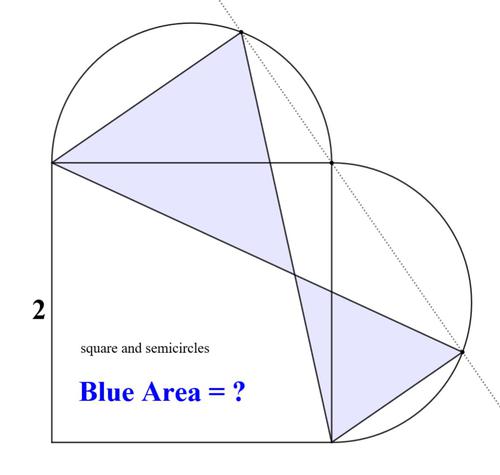
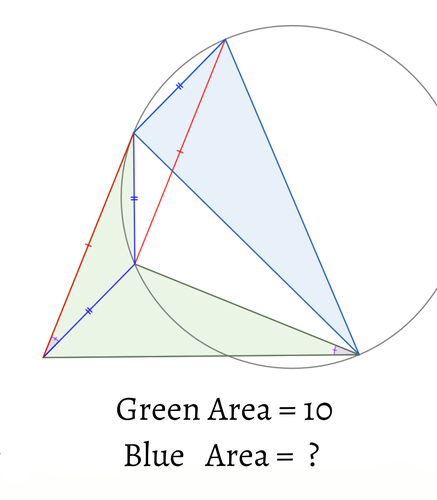
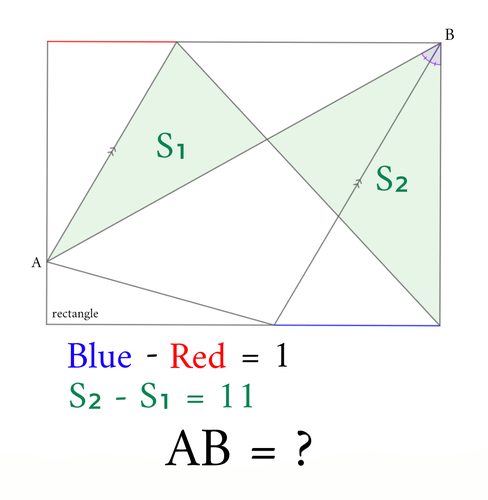
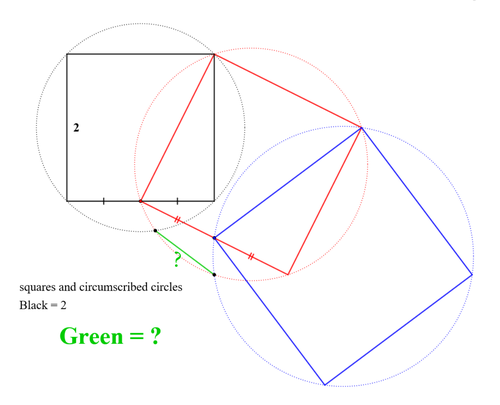
図のように長方形や直角三角形の内接円が配置されています。青で示した角の角度を求めてください。
解答形式
度数法で求め、半角数字で0以上360未満の整数を解答してください。
※度や°などの単位は付けないでください。
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています