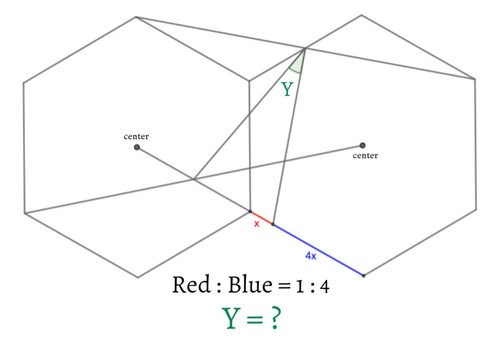
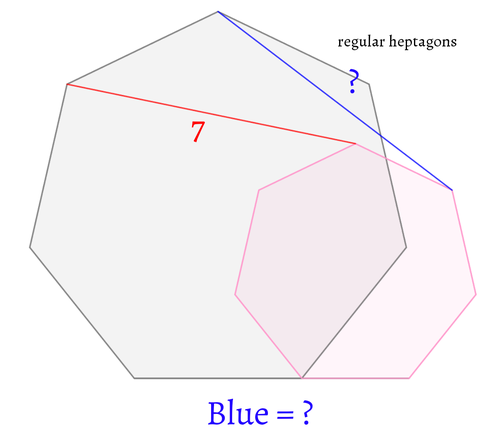
三角形の3等分点と垂線がつくる六角形

【補助線主体の図形問題 #014】
今回は面積関係を問う問題にしてみました。補助線が活躍するのはいつも通り。暗算での処理も可能です。思い思いの解法をお楽しみください。
解答形式
${
\def\cm{\thinspace \mathrm{cm}}
\def\mytri#1{\triangle \mathrm{#1}}
}$ 解答は小数第3位を四捨五入して、小数第2位までを単位なしで入力してください。
(例) $12\cm^2$ → $\color{blue}{12.00}$ $10\sqrt{2}\cm^2$ → $\color{blue}{14.14}$ $\dfrac{1+\sqrt{5}}{2} \cm^2$ → $\color{blue}{1.62}$
入力を一意に定めるための処置です。
たとえば答えに無理数を含む場合、$\sqrt{2}=1.41$や$\pi=3.14$などでは必要な桁が足りない場合があるのでご注意ください。
近似値を求める際には、関数電卓やグーグルの電卓機能、Wolfram|Alpha https://www.wolframalpha.com などのご利用をお勧めします。
ヒント内容の予告
- 全体方針
- ヒント1の続き
- その後の方針
- ヒント3の続き
ヒント1
まずは$\mytri{ABC}$と相似な三角形を見つけましょう。
ヒント2
$\mytri{PRT}$だけでなく$\mytri{SUQ}$も$\mytri{ABC}$と相似で、これらの相似比が求まります。これをどう活かしましょうか。
ヒント3
六角形$\mathrm{PQRSTU}$を$\mytri{SUQ}$、$\mytri{PQU}$、$\mytri{RSQ}$、$\mytri{TUS}$と4つに分解します。すると、……。
ヒント4
$\mytri{PQU}$、$\mytri{RSQ}$、$\mytri{TUS}$をうまく組み合わせると……。
スポンサーリンク
解答提出
おすすめ問題
この問題を解いた人はこんな問題も解いています