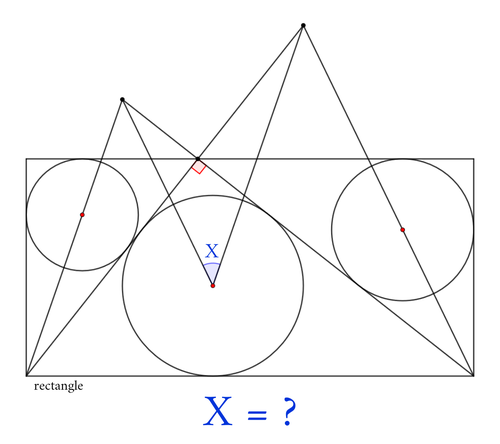
問題文
三角形$ABC$の内部に点$P$があり,$\angle ABP=42^\circ$,$\angle CBP=42^\circ$,$\angle ACP=6^\circ$,$\angle BCP=12^\circ$がそれぞれ成り立っている.このとき,$\angle BAP$の大きさを度数法で表すと,$x^\circ$となる.
$x$に当てはまる数を求めよ.
解答形式
解答のみを,半角数字で答えてください.
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています