全問題一覧

問題文

三角形 $ABC$ の外接円の半径は $2026$ です．この三角形の垂心を $H$ とするとき $AH^2+BC^2$ を求めてください．

問題文

$$x^2+2027x+a$$$$x^2+2026x+b$$
この２つの二次方程式に共通の解が１つある時、最小の自然数a、b、それぞれの値を求めない。

解答形式

1行目にaの値を、2行目にbの値を入力してください。いずれもa=、b=は必要ありません。

問題文

完全数たる半素数を全て求めよ。

註

完全数：その数自身を除く正の約数の総和が，その数自身に等しい数。e.g. $28=1+2+4+7+14$
半素数：$2$ つの素数の積で表される数。

解答形式

解が複数ある場合には，小さいものから順に並べ，半角のカンマ「,」で区切り入力してください。スペースは不要です。

問題文

ある素数$p$に$1$を足したところ、平方数になりました。このような$p$としてあり得る値を全て求めてください。

解答形式

$p$としてあり得る値の総積を求めてください。

問題文

あなたは今日突然術式が覚醒し, 任意の結界で死滅回遊への参加を宣誓することになりました。
死滅回遊に参加したあなたは$1$日に$1$度だけ敵に遭遇し, 各日の遭遇については, 遭遇した敵が術師である確率が $\dfrac{1}{3}$, 非術師である確率が $\dfrac{2}{3}$ である。
あなたは各日 $k＝1,2,…,19$ について, 遭遇する前に確率 $p_k (0<p_k \leqq 1)$ を取り, 以下のゲームを考える。

・その日に術師と遭遇した場合, $\sqrt{p_k}$ で勝利し, 勝てば$5$点を奪うことができる。負けた場合$5$点奪われることになる。
・その日に非術師と遭遇した場合, $\sqrt{1-p_k}$ で勝利し, 勝てば$1$点を奪うことができる。同様に負けた場合$5$点奪われることになる。

$19$日間の総得点の期待値の最大値を求めてください。また, 期待値が最大となるときの $p_k$ を答えてください。

解答形式

求める期待値の最大値は互いに素な正整数 $a,c$, 平方因子をもたない $b$, 正整数 $d$ を用いて $\dfrac{a\sqrt{b}}{c}-d$ と表せるので, $a+b+c+d$ の値とその後ろに $p_k$ の分母と分子の和をすべて半角で入力してください。
※空白はいりません。
例: 最大値が $\dfrac{2\sqrt{3}}{5}-4$ で, そのとき $p_k=\dfrac{1}{2}$ の場合 → $143$

問題文

三角形$ABC$について,外心を$O$,垂心を$H$とするとき,

$BC=2026$,$OH=777$,$BC \parallel OH$が成立した.

直線$AC$上に点$D$を,直線$AB$上に点$E$を,$BD=CE=BC$となるようにとる. ($D,E$は$B,C$とは異なる)

このとき，$DE$の長さを求めよ．

解答形式

$DE$の長さは互いに素な自然数$a,b$を用いて

$\sqrt{\frac{a}{b}}$と表されるため，$a+b$の値を半角数字で解答してください．

問題文

次の式を因数分解せよ。

$$
x^2 +x^4+y^4+3x^2y^2 + xy + 2xy^3 + y^2 - 12 + 2x^3y
$$

解答形式

正解においてそれぞれのカッコ内の定数項の合計の値を解答しなさい。
なお、値が負の数になった場合、-の記号はカタカナで答えなさい。
(例)[ただし◯、◻︎、◎などの記号はx、yなどを含める式を表す]
(◯+2)(◻︎+1)→3
◎(◯-1)(◻︎+3)(△-⭐︎)→2
(◯-2)(◯-3)→マイナス5

問題文

次の問いに当てはまるx値を求めよ

この式はx/3になる
$$ \frac{2027^{2027} - 2027}{2027^{2026} - 1} + \left( \frac{2026^{2} + 2026}{2027} - 2026 \right)^{2027}$$

解答形式

x=は必要ありません。xに当てはまる数値のみ解答すれば良いです。

問題文

$a_{1}+a_{2}+a_{3}+...+a_{100}=100$を満たす100個の非負整数の組$a_{1},a_{2},a_{3},...,a_{100}$の全てについて、
$$\frac{1}{a_{1}!a_{2}!a_{3}!...a_{100}!}$$の総和を求めてください。

解答形式

答えが異なる自然数a,bを用いてa^b/b!という形で表されるため、a+bを回答してください。

問題文

平面上に鋭角三角形ABCがある。以下の条件をみたすように点Dを定める。
「$AB^{2}+BC^{2}+CA^{2}=2CD^{2}$
　$BC=AD$
　$点Dと点Bは直線ACに関して反対の向きにある$」
ここで線分ACを直径とする円と線分AD,BCとの交点をそれぞれE,Fとおき、
直線ACとEFの交点をPとするとAC=100,EF=90が成立した。
このとき、線分APの長さを求めよ。

解答形式

互いに素な正の整数p,qを用いてp/qと表されるので、p/qと解答してください

問題文

正十二角形ABCDEFGHIJKL があります。
袋の中に A〜L までの文字が書かれた12枚のカードが入っています。この袋からカードを1枚引いては戻す作業を 5回 繰り返します。
引いたカードに記された頂点同士を、円周上の順番に従って結び、多角形を作ります。ただし、以下のルールに従うものとします。
同じ頂点を複数回引いた場合は、1つの頂点としてカウントする。
選ばれた頂点の種類が2種類以下の場合は、多角形ができないものとして面積を0とする。
結んだ線分が多角形の内部で交差しないよう、頂点を結ぶ。
このとき、形成された多角形の面積が、もとの正十二角形の面積のちょうど 1/3 になる確率を求めなさい。

解答形式

解答はx/yと表せられるのでx+yの値を答えなさい

問題文

以下の表はある旧帝一工(前期)で過去に出題された数学の問題に出てくる関数の増減表である。
出題された年度と大学名を答えてください。
$※$ $f(x)$ とは私が勝手に置いたものです。

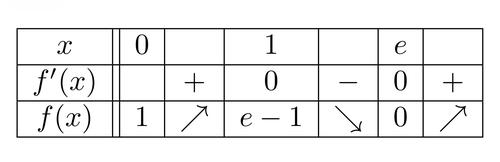
・インターネット上の過去問サイトに掲載されている旧帝一工(医科歯科を除く)の問題です。
・過去問データベースなどで問題を確認したり，検索してみても構いません。
・ヒントと称していますが，ヒントがないと一意に定まらない場合があります。

解答形式

年度と大学名を答えてください
例) 年度は半角数字です。
2026年大阪大学
2026年九州大学
2026年京都大学
2026年東京工業大学
2026年東京大学
2026年東北大学
2026年名古屋大学
2026年一橋大学
2026年北海道大学