数学の問題一覧

問題文

枝と葉からなる $2$ 次元的な植物を考えます。植物は，以下の条件を満たすような枝 $s$ 本と葉 $l$ 枚からなります。

条件

1. $s, l$ は $0$ 以上の整数である。
2. 枝の両端の点には，枝または葉が $0$ 個以上つながっている。
3. すべての枝からたどりつくことができるような，根とよばれる点がただひとつ存在する。
4. 枝がループを作るようにつながっていることはない。

この植物の重さ $n$ は $n=2s+l$ で表されます。例えば，重さ $4$ の異なる植物をすべて描いたものは下図のようになります。

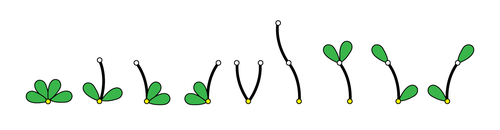ここで，ある点に着目したときに，その点から出ている葉と枝の並びが異なるものは区別することに注意しましょう。

重さ $n$ の植物が $t_n$ 種類あるとき
\begin{equation}
\sum_{n=0}^{\infty}\frac{t_n}{3^n}
\end{equation}の値を求めなさい。ただし，級数が収束することは証明なしに用いてかまいません。

解答形式

答えは正の有理数 $r$ です。

• $r$ が整数ならば，$r$ を半角数字で出力してください。
• $r$ が整数でないならば，互いに素な自然数 $a, b$ を用いて $r=\displaystyle{\frac{a}{b}}$ と表し，$a$ を $1$ 行目に，$b$ を $2$ 行目にそれぞれ半角数字で出力してください。

問題文

$2024!$の約数の和は$2025$の倍数であることを示せ。

間違えて公開してしまい、回答を一件いただいているので、泣く泣くボツ問としてここに供養します。

$\min(f(x))$を関数$f(x)$の$-\frac{\pi}{2}\leq x\leq\frac{\pi}{2}$における最小値とする。
以下の値を求めよ。
$$\int^{16}_0\min(\tan^2{x}+a\cos{x})da$$
ただし$a$と$x$は独立している。

$$
|2^{n-1}+1|
$$
$$
nが、整数のとき、上の式は、必ず（α）である。
$$
$$
(1)負(2)正
$$

$$
||||||||\sqrt{i}^{1024}||||||||
$$
$$
答えはどれ？
$$
$$
(1)1(2)-1(3){i}(4)-{i}
$$

問題文

直角三角形Nの頂点A,B,Cをそれぞれ中心とする円Cp,Cq,Crがあり、それぞれ半径はRp,Rq,Rr(Rp<Rq,Rp<Rr)
直角三角形Nの周の長さを2ab(a,bは互いに素)とします。Rp,Rq,Rr,a,bは自然数。円Cpと円Cq,円Cqと円Cr,円Crと円Cpはそれぞれ接しています。
a<b<2aのとき、Rpをa,bを用いて表してください。

解答形式

半角英数で答えてください。

問題文

正$n$角形$A_1,A_2,\cdots,A_n$と，同じ平面上に点$X$があって$$A_1^2= A_2^2+\cdots+A_n^2 $$を満たしている．このような点$X$が存在する最大の自然数$n$を求めよ．

解答形式

$n$の値を半角数字で1行目に入力してください。

$$
|{\sqrt{i^2}-\sqrt{2i^2}}||{\sqrt{i^2}+\sqrt{3i^2}}||{\sqrt{2i^2}-\sqrt{4i^2}}||{\sqrt{2i^2}+\sqrt{4i^2}}|\\を求めて下さい。
$$
$$
(1)24(2)36(3)42(4)54
$$

$$
|tan2250°・cos1800°・sin1200°|\\を求めて下さい。
$$
$$
(1)\frac{1}{2}(2)\frac{\sqrt{3}}{2}(3)1(4)2
$$

$$
\sqrt{\sqrt{\sqrt{\sqrt{\sqrt{\sqrt{m}^{1024}}}}}}=log_{3}{81}\\について、大さい方の解αについての\\{α}^2＋4α＋4を求めて下さい。
$$
$$
(1)4(2)8(3)12(4)16
$$

問題文

$a=e^{2AX},c=e^{2CX}$(Xは正の定数，A，Cは実数)とする．
$f(x)=-a\log_e(x+c)+X$とする．$y=f(x)$の$y$切片を点P，
$y=f(x)$と点$(0,X)$で接する接線$l$と$y$軸とが成す角を
$\theta\;(\theta\mbox{は}0<\theta<\dfrac{\pi}{2}\mbox{を満たす実数})$，$y=f(x)$の$x$切片を点Qとする．
$\tan\dfrac{\theta}{2}$をネイピア数$e$を用いて表せ．
また，点Qの$x$座標が正の無限大に大きくなるとき，$\tan\dfrac{\theta}{2}$の値の極限値を求めよ．

解答形式

記述式解答を求む．(直感で答えが出る可能性があるので)

2=1
4=11
8=7
25=6
42=21
100=□

ヒント
数字を変換してください。