数学の問題一覧

訂正とお詫び

（2022年1月28日23時17分）
　出題から3週間余り、問題文に不正確な記述がありました。お詫びするとともに上記のように訂正いたします。不要に迷ってしまった方もいらっしゃるかもしれません。申し訳ございませんでした。
　なお、修正前の問題文をご覧になりたい場合はこちらからどうぞ。
https://twitter.com/tb_lb/status/1478365250269622276

${}$　西暦2022年問題第4弾です。今回は2022が満たす性質をちょいと替えてみるという手法で問題を作ってみました。ド根性ではなく、できるだけ計算の手間が減るような解法を楽しんでもらえたら嬉しいです。

解答形式

${}$　解答は$n$の値をそのまま入力してください。「$n=$」の記載も不要です。
（例） $n=104$ → $\color{blue}{104}$
　なお、やや面倒な計算が待っています。必要に応じてWolfram|Alphaや関数電卓などを遠慮なくご利用ください。

【補助線主体の図形問題 #079】
　先週今週と2週続けて内心と傍心をテーマにした問題をお送りしています。補助線次第では暗算可能です。挑戦をお待ちしております！

解答形式

${\def\cm{\thinspace \mathrm{cm}}}$　解答は小数第3位を四捨五入して、小数第2位までを単位なしで入力してください。
（例） $12\cm$ → $\color{blue}{12.00}$　　$10\sqrt{2}\cm$ → $\color{blue}{14.14}$　　$\dfrac{1+\sqrt{5}}{2} \cm$ → $\color{blue}{1.62}$
　入力を一意に定めるための処置です。
　たとえば答えに無理数を含む場合、$\sqrt{2}=1.41$や$\pi=3.14$などでは必要な桁が足りない場合があるのでご注意ください。
　近似値を求める際には、関数電卓やグーグルの電卓機能、Wolfram|Alpha https://www.wolframalpha.com などのご利用をお勧めします。

問題文

各文字が < か > であるような長さ $13$ の文字列 $S$ の内, 次の条件を満たす整数列 $a_1, a_2, \cdots a_{14}$ が一意に存在するようなものはいくつありますか？
・$S$ の $i$ 文字目が < ならば, $a_{i+1} = a_i + 1$
・$S$ の $i$ 文字目が > ならば, $a_{i+1} = a_i - 1$
・$1 \leq a_k \leq4 \ (k = 1, 2, \cdots, 14)$

解答形式

半角数字で解答して下さい.

問題文

図の条件の下で、線分 $CG$ の長さを求めてください。
※図中の各線分の長さの比は正確とは限りません。

解答形式

互いに素な正整数 $a,b$ によって $CG=\dfrac{a}{b}$ と表せるので、$a+b$ の値を半角数字で解答してください。

問題文

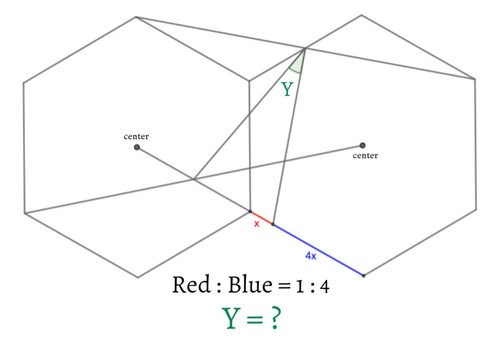
正六角形2つが図のように配置されています。赤い線分と青い線分の長さの比が1:4であるとき、緑で示した角Yの角度を求めてください。
ただし、図中"center"で示した点は正六角形の外心です。

解答形式

0~360までの半角数字で、「°」や「度」をつけずに解答してください。

$a!+b!+5c^2=2024$となる自然数$a,b,c$の組$(a,b,c)$を全て求めよ。

＊＊入力形式＊＊
(a,b,c)=(1,1,1),(2,3,4),...というふうに半角で入力してください。区切る時は,を用いてください。(順不同)

問題文

$1,2...nの数字を次の条件を満たすように一列に並べる方法の数をa_nとする。$
$条件:k(k=1,2,...n-1)について右隣の数がk+1でない。$
$このとき、a_7を求めよ。$

解答形式

半角数字で回答してください。
4/19追記この問題は、改善点があるので、工事予定です。

問題文

正六角形内に、図のように円を配置しました。青で示した角の大きさを求めてください。

解答形式

$\angle x=a°$ です。$a$ に当てはまる0以上180未満の数値を半角で回答してください。

問題文

以下の値を求めてください。
$$
\sum_{1\leqq m<n\leqq 9} \biggl(\cos\dfrac{m\pi}{10}+\cos\dfrac{n\pi}{10}+1\biggr)^3
$$

解答形式

答えは正整数になるので、それを半角数字で解答してください。

問題文

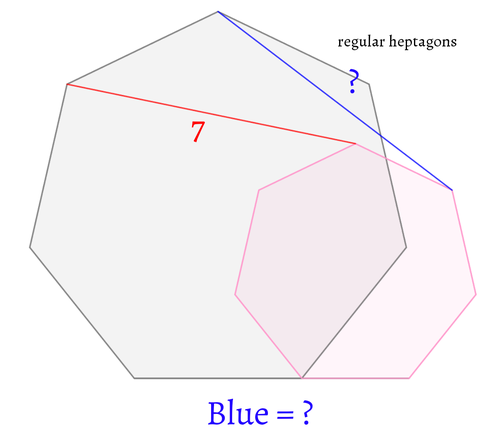
正七角形2つが図のように配置されています。
赤色の線分の長さが7のとき、青色の線分の長さを求めてください。

解答形式

半角数字で解答してください。

${}$　西暦2023年問題第4弾です。今年の西暦問題も折り返しとなりました。桁数が大きいですが、手計算で処理できるよう仕込んであります。どうぞお楽しみください。

解答形式

${}$　解答は、$N$の値をそのまま入力してください。「$N=$」の記載は不要です。
（例） $N=2323232323$ → $\color{blue}{2323232323}$

問題文

$f:{\mathbb R} \rightarrow {\mathbb R}$ は微分可能で、任意の $x,y \in {\mathbb R}$ に対して

$$
f(x+y)+f(x)f(y)=f(xy+1)
$$

を満たすとする。以下の空欄を埋めよ。

⑴ $f(0)=\fbox{アイ}$ または $f(0)=\fbox{ウ}$ が成り立つ。また、$f(0)=\fbox{アイ}$ のとき $f(1)=\fbox{エ}$ で、このとき $x \in {\mathbb R}$ を固定するごとに極限

$$
f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}
$$

を考えるとロピタルの定理の仮定をすべて満たしていることがわかる。よって同定理を用いて $f$ が満たす微分方程式を導くことができる。

⑵ $f$ が満たす微分方程式を解くことで、$f$ をすべて決定できる。特に $f(23)$ がとり得る値は $\fbox{オ}$ 通りあり、それらの値の総和は $\fbox{カキク}$ である。

解答形式

ア〜クには、0から9までの数字または「-」(マイナス)が入る。
⑴の答えとして、文字列「アイウエ」をすべて半角で1行目に入力せよ。
⑵の答えとして、文字列「オカキク」をすべて半角で2行目に入力せよ。