数学の問題一覧
問題文
実数列 $\lbrace a_n \rbrace_{n = 1, 2, \cdots 2024}$ が以下を満たしています.
・ $a_0 = 0$
・ $0 \leq a_n \leq n+1$
・ $a_{2024} = 2025$
このとき,
$$\sum_{n = 1}^{2024} \sqrt{{a_{n-1}}^2 + {a_{n}}^2 - a_{n-1}a_n - 2na_{n-1} + na_n + n^2}$$
には最小値が存在するため, 最小値を取るときの $a_{1000}$ の値を求めて下さい. ($a_{1000}$ の値は一意に定まります.)
解答形式
答えは, 互いに素な正整数 $a, b$ によって $\cfrac{b}{a}$ と表されるため, $a+b$ の値を解答して下さい.
問題文
鋭角三角形 $ABC$ に対し,重心と垂心をそれぞれ $G,H$ とし,直線 $GH$ と辺 $AB,AC$ との交点をそれぞれ $D,E$ とし,直線 $AH$ と辺 $BC$ の交点を $F$ としたところ,$DH:HG=4:3,BF:FC=3:7$ となりました.
${AD}^2:{AE}^2$ は互いに素な正の整数 $a,b$ を用いて $a:b$ と表されるので,$a+b$ の値を求めてください.
解答形式
半角数字で解答してください.
問題文
(2020.9.26 11:57追記)
解答形式に不備があったため、訂正致しました。
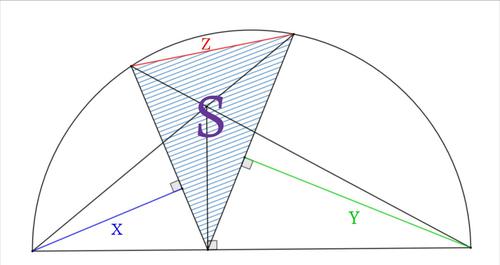
図の青、緑、赤の線分の長さを$X,Y,Z$、斜線部の面積を$S$とすると、次の式が成り立つ。
$$
\frac{[ア]}{S}=\frac{[イ]}{Z}\left(\frac{1}{X}+\frac{1}{Y}\right)
$$
なお、図の曲線は半円の弧である。
解答形式
$[ア],[イ]$にはともに自然数が入ります。その和を半角数字で解答してください。
ただし、その和が最小となるように解答してください。
例:$[ア]=4,[イ]=2$なら$6$ではなく(両辺を$2$で割ることにより)$3$と解答。

【補助線主体の図形問題 #072】
今週の問題は久しぶりに求角問題です。地道に角度を求めていけば手掛かりが見つかるかもしれません。自信のある方は、できるだけ少ない計算回数で、かつ、暗算で挑戦してみてください!
解答形式
${\renewcommand\deg{{}^{\circ}}}$ 解答は小数第3位を四捨五入して、小数第2位までを単位なしで入力してください。角度は弧度法ではなく度数法で表すものとします。
(例) $12\deg$ → $\color{blue}{12.00}$ $\frac{360}{7}^{\circ}$ → $\color{blue}{51.43}$
入力を一意に定めるための処置です。
近似値を求める際には、関数電卓やグーグルの電卓機能、Wolfram|Alpha https://www.wolframalpha.com などのご利用をお勧めします。
問題文
図1は、あるへこみのない立体の展開図です。図1は合同な正方形2個、合同な菱型4個、合同な台形8個からなり、これを組み立てると2個の正方形1組がたがいに向かい合い、2個の台形4組がたがいに向かい合い、2個の菱形2組がたがいに向かい合います。また、図2は図1に使われている3種類の図形を、1目盛りが1cmの方眼用紙に描いたものです。図1を組み立ててできる立体の体積は何cm$^3$ですか。
図1

図2

解答形式
四捨五入して整数で答えてください。
例)$\frac{17}{4}cm^3$→4
${}$ 西暦2023年問題第3弾です。今回は数列から2023の位置を問うという、入試問題にありがちなテーマ設定にしてみました。問題文はあえて小難しく書いてますが、数列の規則性をとらえられれば十分です。軽く解いてやってください。
解答形式
${}$ 解答は、$a_{n}=2023$となる$n$の値をそのまま入力してください。なお、$a_{n}=2023$となる$n$が存在しない場合には「-1」と入力してください。
(例) $a_{103}=2023$ → $\color{blue}{103}$
問題文
$p$を$0$以上$1$以下の実数とします.$A$と$B$の二人は,円形の的を用いて次のようなダーツ遊びをします.
- $A,B,A,B,\dots$の順に,的に向かって交互に矢を投げる.
- $A$は直前に$B$が投げた矢よりも中心に近い位置に矢が刺されば成功となる.ただし$1$回目は必ず成功とみなす.
- $B$は直前に$A$が投げた矢よりも中心から遠い位置に矢が刺されば成功となる.
- $n$回目に矢を投げたプレイヤーは,成功すると$p^n$点を得る.成功しなかった場合,その時点でゲームを終了する.
矢の刺さる位置が的の中で一様ランダムに決まると仮定するとき,ゲームが終了するまでに$A$が得られる得点の期待値を$f(p)$とし,$B$が得られる得点の期待値を$g(p)$とします.$f(p)=\dfrac{20}{21}$であるとき,$g(p)$の値は互いに素な正整数$a,b$を用いて$\dfrac{b}{a}$と表せるので,$a+b$を解答してください.
解答形式
半角数字で入力してください.
問題文
以下の漸化式で与えられる数列${a_n},{b_n}$を考える。ただし、$n$は非負整数であるとし、${a_n}$の初項は$a_0=1$とする。
$\displaystyle a_{n+1}=\sum_{k=0}^na_ka_{n-k} , \displaystyle b_{n+1}=\sum_{k=0}^n (k+1)a_ka_{n-k}$
(1)$b_n$を$a_n$で表わせ。
(2)$\displaystyle a_{n+1}=\frac{2(2n+1)}{n+2}a_n$を証明せよ。
(3)それぞれの数列の一般項$a_n,b_n$を求めよ。
(4)$\displaystyle \lim_{n \to \infty} \sqrt[n]{a_n}$を求めよ。ただし$\displaystyle\lim_{n \to \infty} \frac{\log n}{n}=\lim_{n \to \infty} \frac{\log(n+1)}{n}=0$を証明無しで用いても良い。
解答形式
(4)の答えを半角数字またはTeXで入力してください。
(1)~(3)についてはお手持ちの紙に解答し、解説を確認ください。
問題文
四角形$ABCD$があります.線分$AC$上に点$P$を,線分$BP$上に点$Q$を,線分$DP$上に点$R$を取ります.直線$AQ$と線分$BC$,直線$CQ$と線分$AB$,直線$AR$と線分$CD$,直線$CR$と線分$AD$の交点をそれぞれ$S,T,U,V$とします.
$$\triangle BSA=(四角形BSPT)+8=\triangle BCT+12
\\\\\triangle AUD =30,\triangle CDV=25$$
が成り立つとき四角形$DVPU$の面積を求めてください.
解答形式
求める値は互いに素な自然数$p,q$を使って$\cfrac{q}{p}$と表されるので$p+q$の値を答えてください.
$$
log_3\frac{27^n}{{9}^{n^2}}における,n,最大値を求めて下さい。
$$
$$
(1)\begin{cases}最大値\frac{1}{3}\\(n=\frac{1}{3})\end{cases}
(2)\begin{cases}最大値\frac{2}{3}\\(n=\frac{5}{6})\end{cases}
(3)\begin{cases}最大値\frac{5}{6}\\(n=\frac{2}{5})\end{cases}
(4)\begin{cases}最大値\frac{9}{8}\\(n=\frac{3}{4})\end{cases}
$$