全問題一覧
問題文
曲1
僕何回
何年
共終
仕方
思零言葉違
曲2
僕何回何十回
君抱合手繋
思出度想出
君作
何回何十回謝
感謝言葉忘
危険性少高
許
解答形式
2曲のタイトルをひらがなで、スペースを空けずに並べて1行で解答してください.
問題文
忘時流
心君笑小丸
穴何見
一人叶夢
君声抱歩
僕届
探君会日今懐言葉
向水玉雲散日
風吹飛軽
他人同幸信
傷誰傷
僕届
瞬長季節来
呼合名前始
聴
君声抱歩
僕届
君声抱歩
僕届
君声
解答形式
ひらがなで解答してください.
問題文
円に内接する四角形 $ABCD$ があり,$\angle ABC = 90^\circ$ をみたしている.$2$ 点 $A , C$ を通り直線 $AB$ に接するような円と線分 $BD$ の交点を $E$ とすると,$CD = CE$ が成立した.$BE = 7 , ED = 9$ であるとき,線分 $AB$ の長さの2乗を求めよ.
解答形式
半角数字で解答してください.
問題文
$AB=44,AC=46$ をみたす三角形 $ABC$ があり, $AB,AC$ の中点を $M,N$ とする. 三角形 $ANB$ の外接円と三角形 $AMC$ の外接円の $A$ でない交点を $P$ とすると $P$ が線分 $BC$ 上に存在した.
このときの線分 $BC$ の長さを求めよ
解答形式
$BC^2$ は正の整数値になるので, その値を半角で解答してください
問題文
$y=xe^x$の第$n$次導関数を$y^{(n)}$とし,
そのグラフの変曲点の$y$座標を$Y_{n+1}$とおく。
$\sum_{k=1}^{\infty} Y_k$
を求めよ。ただし,答えのみ記せ。
問題文
「正方形と正三角形 Part1」に続いており、誘導のようになっているため、Part1を解いていない方は先にPart1を解いておくことをお勧めします♪
誘導なしでもデキルケド、、、
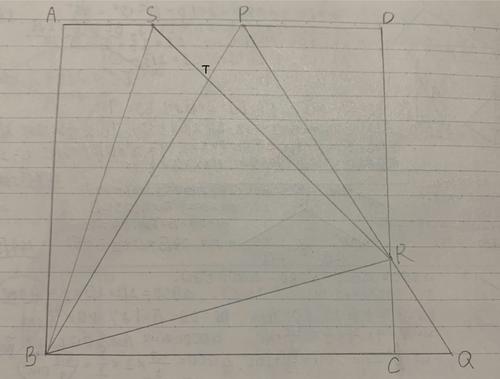
四角形ABCDは正方形である。辺AD上に点P、BCの延長線上に点Qを取ると、三角形PBQは正三角形になる。DCとPQの交点をRとする。AP上にSを取ると三角形SBRも正三角形になる。次の問いに答えなさい。
SRとPBの交点をTとする。SBはSTの何倍であるか答えなさい。
解答形式
◯倍のような「倍」はつけずに数字や記号のみで答えてください。√、+、-などを使う場合はカタカナで表記してください。2+√2のように、√の数よりも先に2などの整数を答えてください。√同士であれば、中身の数が少ない順に答えなさい。
√→ルート
+→プラス
-→マイナス
(例)3
2ルート3
3マイナスルート2プラスルート3
問題文
あなたのやのが
かなにんでえた
しのの
っけすぎたの
あなたがそばにいないので
ってほどのささをた
らないいやの
おどけてったそのの
もいないかない
いえないいえないな
りでいいやなんて
そうをしてるいについて
えてえてもそばにいれるように
ってってってそうやって
きっとにかかったようにはりわって
このにちこめたえないを
おいしそうによくんであなたはのみんだ
それにどれだけわれたことかあなたはらないな
えたらそのときはになれたらいいな
あなたのやが
かなにんでえた
にしてったい
してきげた
りつめたのれた
いえないいえないな
いになったよなんて
そうをしてのについて
ずかしがらないであなたにえるように
ってってってそうやって
やっとにすようになれたをって
りげたのそのをって
しそうにをいてにししたんだ
それにどれだけわれたことかもしもあなたがってても
えたらそのときはにできたらいいな
もう
ってってってそうやって
きっとにかかったようにはりわって
このにちこめたえないを
おいしそうによくんであなたはのみんだ
それにどれだけわれたことかあなたはらないな
えたらそのときはになれたらいいな
解答形式
カタカナで解答してください.