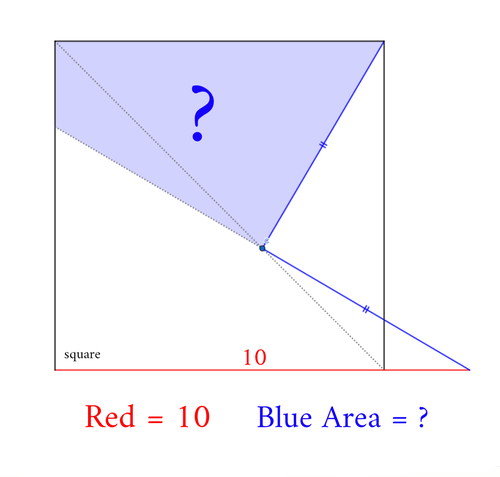
解説
$$
\newcommand{\nc}{\newcommand}
\nc{\wake}[1]{\begin{cases} #1 \end{cases}}
\nc{\f}[2]{\dfrac{#1}{#2}}
\nc{\s}[1]{\{#1\}}
\nc{\pmat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\nc{\lr}[1]{\left( #1 \right)}
\nc{\com}[2]{{}_{#1}{\rm C}_{#2} \right)}
\nc{\bar}[1]{{\overline{#1}}}
\nc{\bb}[1]{{\mathbb {#1}}}
\nc{\rmn}[1]{{\rm #1}}
\nc{\q}{\quad}
\nc{\x}{\times}
\nc{\a}{\alpha}
\nc{\b}{\beta}
\nc{\th}{\theta}
\nc{\Q}[1]{\fbox{#1}}
$$
$\rm C,B$ の中点を $\rm M$ とし、 $2n$ 秒後に $\rm M$ を右向きに通過している確率を $R_n,$ 左向きに通過している確率を $L_n$ とおくと
$$
A_{n+1}=\f{25}{36}A_n+\f{1}{6}D_n+\f{5}{6}L_n\\
D_{n+1}=\f{25}{36}D_n+\f{1}{6}A_n+\f{5}{6}R_n\\
L_{n+1}=\f{5}{36}D_n+\f{1}{6}R_n\\
R_{n+1}=\f{5}{36}A_n+\f{1}{6}L_n
$$
これらを上から順に $(1),\cdots,(4)$ とする。 $(1)+(2),(1)-(2),(3)-(4)$ を作り
$$
A_n+D_n+L_n+R_n=1
$$
を用いることで
$$
X_{n+1}=\f{31}{36}X_n+\f{5}{6}(1-X_n)=\f{1}{36}X_n+\f{5}{6}\\
Y_{n+1}=\f{19}{36}Y_n+\f{5}{6}Z_n\\
Z_{n+1}=-\f{5}{36}Y_{n}-\f{1}{6}Z_n\\
$$
を得る。ただし $X_n=A_n+D_n,Y_n=A_n-D_n,Z_n=L_n-R_n$ とおいた。さらに $Z_n$ を消去することによって
$$
X_{n+1}=\f{1}{36} X_n+\f{5}{6}\\
Y_{n+2}-\f{13}{36}Y_{n+1}+\f{1}{36}Y_n=0
$$
を得る。初期条件は $X_0=1,Y_0=1,Y_1=\f{19}{36}$ であるので、この下で漸化式を解いて
$$
A_n=\f{X_n+Y_n}{2}=\f37+\f1{14}\lr{\f1{36}}^n-\lr{\f{1}{9}}^n+\f{3}{2}\lr{\f{1}{4}}^n
$$
を得る。
おすすめ問題
この問題を解いた人はこんな問題も解いています