問題文
※解答形式に注意!
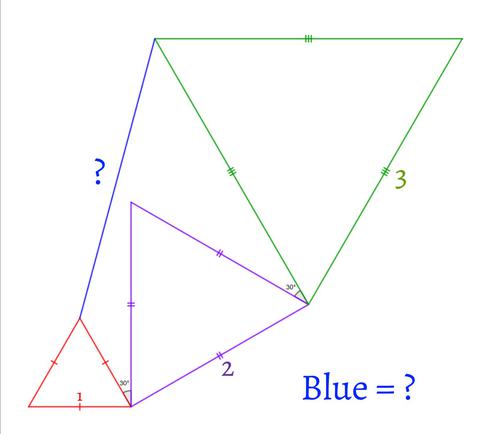
図のように配置された3つの正三角形があります。青い線分の長さを求めてください。
ただし、赤、紫、緑の線分の長さはそれぞれ1,2,3で、隣り合う正三角形の間の角は30°です。
解答形式
答えは自然数$A,B$を用いて$A\sqrt{B}$の形に表せます。$A+B$を解答してください。
ただし、根号の中はできるだけ小さい自然数にしてください。
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています