問題文
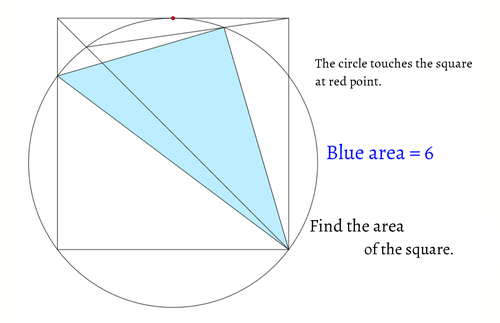
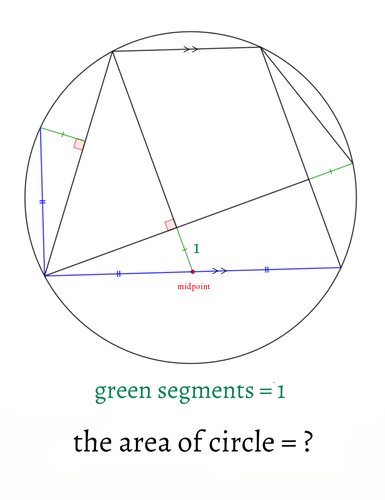
緑色の線分の長さは1です。
このとき、円の面積を求めてください。
図中の赤点はそれを含む線分の中点です。
解答形式
答えは(分数)×πの形になります。
分子を1行目に、分母を2行目に半角数字で入力してください。
ただし、既約分数の形で解答してください。
例: (10/3)π → 1行目に10、2行目に3
ヒント1
補助線は要りません。
スポンサーリンク
解答提出
この問題は自動ジャッジの問題です。
解答形式が指定されていればそれにしたがって解答してください。
おすすめ問題
この問題を解いた人はこんな問題も解いています