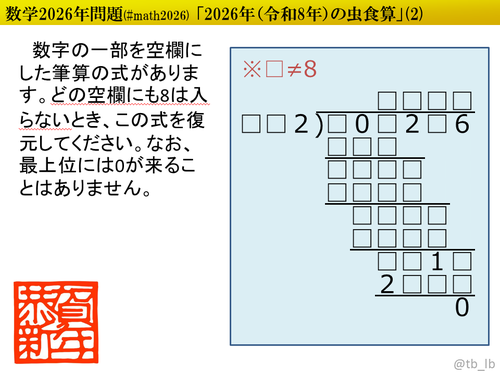
2026年（令和8年）の虫食算(2)

${}$　西暦2025年問題第2弾です。第1弾に引き続き虫食算で、今回は割り算にしてみました。数学的手法（約数や倍数、偶奇性や剰余、不等式による絞り込み、などなど）を適宜用いることで面倒な場合分けや仮置きを軽減できるよう仕込んでいるのは変わりません。パズル的に解くのもよし、数学的にゴリゴリ解くのもよし、どうぞお好きなようにお楽しみください！

解答形式

${}$　解答は2行目を「被除数÷除数」の形で入力してください。
（例） $2026 \div 102 = 19$ 余り $88$ → $\color{blue}{2026 \text{÷} 102}$
　入力を一意に定めるための処置です。数字は半角で、「÷」の演算記号はTeX記法（\div）でも、絵文字や環境依存文字でもなく、全角記号の「÷」でお願いします。空白（スペース）も入れる必要はありません。