解説
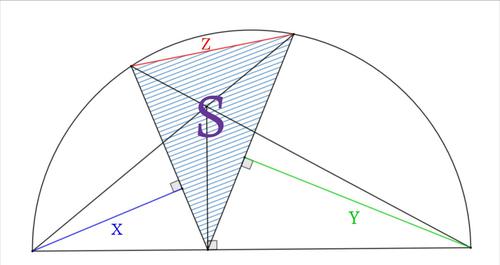
$△XYZ$について、$X=\pi-2A,Y=\pi-2B,Z=\pi-2C$である。また、一般に$△ABC$について外接円の半径を$R$、内接円の半径を$r$とすると次の式が成り立つ。
$$
r=4R\sin{\frac A2}\sin{\frac B2}\sin{\frac C2}
$$
これを用いると、$△XYZ$の外接円の半径を$R$として、
$$
r'=4R\sin{\frac X2}\sin{\frac Y2}\sin{\frac Z2}=4R\cos A\cos B\cos C
$$
となり、さらに$△XYZ$の外接円は$△ABC$の九点円であることから$△ABC$の外接円の半径は$2R$となり、
$$
r=4\times2R\sin{\frac A2}\sin{\frac B2}\sin{\frac C2}
$$
が成り立つ。したがって問題の式は以下のように変形される。
$$
\frac{r}{r'}\cos{\frac A2}\cos{\frac B2}\cos{\frac C2}=\frac{R}{4R}\frac{\sin A\sin B\sin C}{\cos A\cos B\cos C}=\frac 14\tan A\tan B\tan C
$$
ここで、$A+B+C=\pi$のとき$\tan A\tan B\tan C=\tan A+\tan B+\tan C$であり、$0\leq x< \frac{\pi}{2}$において$\tan x$が下に凸であることから次のように最小値が求まる。
$$
\frac 14\tan A\tan B\tan C=\frac 14(\tan A+\tan B+\tan C)\geq\frac 34\tan{\left (\frac{A+B+C}{3}\right )}=\frac{3\sqrt3}{4}
$$
おすすめ問題
この問題を解いた人はこんな問題も解いています