[F] Slow and Steady

問題文

$P$ を $n\times n$ 行列とする。$P$ の第 $(i, j)$ 成分と第 $(n-i+1, n-j+1)$ 成分がつねに一致するとき，$P$ を点対称行列と呼ぶことにする。例えば $n=4$ なら，$P$ は一般に

$$
P=\begin{pmatrix} a & b & h & g \\ c & d & f & e \\ e & f & d & c \\ g& h & b & a \end{pmatrix}
$$

という形をしている。$E'$ を $4\times 4$ の単位行列とし，$4\times 4$ 行列 $J'$ を

$$
J'=\begin{pmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{pmatrix}
$$

で定義する。

(1) 一般の $4\times 4$ 行列 $X$ に対して，$XJ'$ の $(\fbox{ア},\fbox{イ})$ 成分と $X$ の $(1,2)$ 成分は一致する。また，$J'X$ の $(\fbox{ウ},\fbox{エ})$ 成分と $X$ の $(1,2)$ 成分は一致する。よって， $4\times 4$ 行列 $P$ が点対称行列であることは，$J'PJ'=P$ が成り立つことと同値である。

(2) $E$ を $2\times 2$ の単位行列とし，$2\times 2$ 行列 $J$ を

$$
J=\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}
$$

で定義する。$4\times 4$ 点対称行列 $P$ が，ある $2\times 2$ 行列 $A,B,C,D$ を用いて

$$
P=\begin{pmatrix} A & B \\ C & D \end{pmatrix}
$$

と表せたとする。(1) と同様の考察より，$D=JAJ, B=JCJ$ である。$4\times 4$ 行列 $Q$ を

$$
Q=\frac{1}{\sqrt{2}}\begin{pmatrix} E & -J \\ J & E \end{pmatrix}
$$

で定めると，$Q^{\rm T}Q=\fbox{オ}$ であり

$$
Q^{\rm T}PQ=\begin{pmatrix} \fbox{カ}+\fbox{キク} & \fbox{ケ} \\ \fbox{コ} & \fbox{サシス}-\fbox{セソ} \end{pmatrix}
$$

が成り立つ。

(3) $p$ を実定数とする。(2) の結果を利用して，行列

$$
P=\begin{pmatrix} 0 & p & 0 & 1-p \\ 0 & p^2 & 1-p & p(1-p) \\ p(1-p) & 1-p & p^2 & 0 \\ 1-p & 0 & p & 0 \end{pmatrix}
$$

の固有値を求めよう。$p=\cfrac{13}{15}$ のとき，$P$ の固有値は大きい順に

$$
\fbox{タ}, \frac{\fbox{チ}}{\fbox{ツ}}, \frac{\fbox{テ}}{\fbox{トナ}}, \frac{\fbox{ニ}}{\fbox{ヌネノ}}
$$

である。

解答形式

空欄 $\fbox{ア}$ 〜 $\fbox{ノ}$ には，半角数字 0 - 9 ，記号 - ，4×4行列 E', J' ，2×2行列 E, J, A, C, O のいずれかが当てはまります（B, Dを使って解答することはできません。O は零行列を表します）。$\fbox{ア}$ 〜 $\fbox{ノ}$ に当てはまるものを改行区切りで入力してください。分数はこれ以上約分できない形で解答してください。

問題文

$n=0,1,\cdots$ に対し，$I_n$を
$$
I_n=\sum_{k=0}^{\infty}\frac{1}{2^{k}k!(2n+2k-1)!!}
$$で定める。ただし $(-1)!!=1$ とする。この級数は収束することが知られている（例えば，ダランベールの判定法を適用すればよい）。特に
$$
I_0+I_1=\fbox{ア}
$$である。また，$\{I_n\}$ は漸化式
$$
I_{n-1}-I_{n+1}=(\,\fbox{イ}\,n-\fbox{ウ}\,)I_n\quad(n=1,2,\cdots)
$$を満たし
$$
\lim_{n\to\infty}\frac{I_{n+1}}{I_n}=\fbox{エ}
$$が成り立つ。これらの結果を用い，漸化式を変形すると
$$
1+\cfrac{1}{3+\cfrac{1}{5+\cfrac{1}{7+\cfrac{1}{\ddots}}}}=\frac{\fbox{オ}^{\fbox{カ}}+\fbox{キ}}{\fbox{ク}^{\fbox{ケ}}-\fbox{コ}}
$$が得られる。ただし $\fbox{オ}\neq\fbox{キ}$ とする。

注意

自然数 $n\geq 1$ に対し，$n!!$ は $1$ 個とばしの階乗を表す。例えば，$n$ が奇数のとき
$$
n!!=n(n-2)(n-4)\cdots 3\cdot 1
$$である。

解答形式

空欄 $\fbox{ア}$ 〜 $\fbox{コ}$ には，半角数字 0 - 9 ，記号 - ，円周率 π ，自然対数の底 e のいずれかが当てはまります。$\fbox{ア}$ 〜 $\fbox{コ}$ に当てはまるものを改行区切りで入力してください。

問題文

片面が黒色、もう片面が白色のオセロが一直線に$N$個並んでいる。1秒経過するごとに，$N$個のオセロから無作為に1つ選び裏返す。

時刻$t(\geq0)$における黒色のオセロの個数を$A_N(t)$で表すとする。$A_4(0)=2$のとき$A_4(2)=2$となる条件付き確率を$P_1$，$A_8(0)=2$のとき$A_8(3)=3$となる条件付き確率を$P_2$とすると，
$$
P_1=\frac{\fbox{ア}}{\fbox{イ}},~~~~P_2=\frac{\fbox{ウ}}{\fbox{エ}}
$$である.

時刻$t(\geq0)$における$A_N(t)$の期待値を$\mu_N(t)$とすると，以下の漸化式が成立する。
$$
\mu_N(t+1)=\left(\fbox{オ}-\frac{\fbox{カ}}{\fbox{キ}}\right)\mu_N(t)+\fbox{ク}
$$これより，
$$
\lim_{t\to\infty}\mu_{50}(t)=\fbox{ケ}
$$となる。

解答形式

空欄 $\fbox{ア}$〜$\fbox{ク}$には，自然数あるいは N が入る。それぞれに当てはまる数字もしくはアルファベットを改行区切りで入力せよ。なお，分数はこれ以上約分できない形にすること。

問題文

漸化式
$$
a_{n+3}=3a_{n+2}-4a_{n+1}+2a_n\quad (n=1,2,\cdots)
$$および
$$
a_1=1, \; a_2=0, \; a_3=0
$$を満たす数列 $\{a_n\}$ を考える。次の空欄 $\fbox{ア}$ 〜 $\fbox{フ}$ に当てはまる数字を答えなさい。

• 漸化式
  $$
  a_{n+3}=3a_{n+2}-4a_{n+1}+2a_n\quad (n=1,2,\cdots)
  $$を満たす数列全体の集合を $V$ とする。数列 $a_n, b_n\in V$ および $c\in\mathbb{C}$ に対して，第 $n$ 項が $ca_n, a_n+b_n$ であるような数列をそれぞれ数列 $a_n$ の $c$ 倍，数列 $a_n, b_n$ の和と定義することにすると，この和とスカラー倍により $V$ は $\mathbb{C}$ 上のベクトル空間になる（確かめよ）。ここで，$V$ の元 $a_n$ は，$a_1, a_2, a_3$ を定めることで完全に決定できる。すなわち，写像 $\varphi: V \to \mathbb{C}^3$ を
  $$
  \varphi(a_n)=\begin{pmatrix} a_1 \\ a_2 \\ a_3\end{pmatrix}
  $$で定めると，$\varphi$ は全単射である。しかも，$\varphi$ は線型写像だから，$\varphi$ はベクトル空間の同型になる。$V$ は $\fbox{ア}$ 次元である。また，$e_n^{(1)}, e_n^{(2)}, e_n^{(3)}\in V$ を
  $$
  \varphi(e_n^{(1)})=\begin{pmatrix} 1 \\ 0 \\ 0\end{pmatrix},\; \varphi(e_n^{(2)})=\begin{pmatrix} 0 \\ 1 \\ 0\end{pmatrix},\; \varphi(e_n^{(3)})=\begin{pmatrix} 0 \\ 0 \\ 1\end{pmatrix}
  $$となるように定めると，$e_n^{(1)}, e_n^{(2)}, e_n^{(3)}$ は $V$ の基底になる。

• $V$ 上の線型変換 $L: V\to V$ を次のように定義する。$a_n\in V$ に対して，$L(a_n)$ を第 $1, 2, 3$ 項がそれぞれ $a_2, a_3, a_4$ である数列とする（$L$ が線型写像になることを確かめよ）。このとき，$L(a_n)$ の第 $n$ 項は $a_{n+\fbox{イ}}$ である。基底 $e_n^{(1)}, e_n^{(2)}, e_n^{(3)}$ のもとでの $L$ の表現行列 $L_A$ は
  $$
  L_A=\begin{pmatrix} \fbox{ウ} & \fbox{エ} & * \\ \fbox{オ} & \fbox{カ} & \fbox{キ} \\ \fbox{ク} & \fbox{ケコ} & \fbox{サ}\end{pmatrix}
  $$である。

• $L_A$ の固有値を $\lambda^{(1)}, \lambda^{(2)}, \lambda^{(3)}$ とする（$\lambda^{(1)}\in\mathbb{R}, {\rm Im}(\lambda^{(2)})>0, {\rm Im}(\lambda^{(3)})<0$）。このとき
  \begin{align}
  \lambda^{(1)}&=\fbox{シ}\\
  {\rm Re}(\lambda^{(2)})={\rm Re}(\lambda^{(3)})&=\fbox{ス}\\
  {\rm Im}(\lambda^{(2)})=-{\rm Im}(\lambda^{(3)})&=\fbox{セ}
  \end{align}である。

• 固有値 $\lambda^{(1)}, \lambda^{(2)}, \lambda^{(3)}$ に対応する固有ベクトルをそれぞれ $\alpha^{(1)}, \alpha^{(2)}, \alpha^{(3)}$ とする。固有ベクトルには定数倍の不定性があるが，$\alpha^{(j)}\;(j=1,2,3)$ の第 $1$ 成分が固有値 $\lambda^{(j)}$ に一致するようにとると
  \begin{align}
  \alpha^{(1)}=\begin{pmatrix} \lambda^{(1)} \\ \fbox{ソ} \\ * \end{pmatrix},\; \alpha^{(2)}=\begin{pmatrix} \lambda^{(2)} \\ \fbox{タ}\;i \\ * \end{pmatrix},\; \alpha^{(3)}=\begin{pmatrix} \lambda^{(3)} \\ * \\ \fbox{チツ}-\fbox{テ}\;i \end{pmatrix}
  \end{align}である。

• $\varphi(\beta_n^{(1)})=\alpha^{(1)}, \;\varphi(\beta_n^{(2)})=\alpha^{(2)}, \;\varphi(\beta_n^{(3)})=\alpha^{(3)}$ となる数列 $\beta_n^{(1)}, \beta_n^{(2)}, \beta_n^{(3)}\in V$ をとる。$\beta_n^{(1)}, \beta_n^{(2)}, \beta_n^{(3)}\in V$ は $V$ の基底をなすから，$V$ の任意の元 $a_n$ はこれらの線型結合で表すことができる。例えば，$a_n\in V$ が
  $$
  a_1=1, \; a_2=0, \; a_3=0
  $$を満たすとき
  $$
  a_n=\fbox{ト}\;\beta_n^{(1)}-\frac{\beta_n^{(2)}-\beta_n^{(3)}}{\fbox{ナ}\; i}
  $$が成り立つ。これを変形すると
  $$
  a_n=\fbox{ニ}-\left(\sqrt{\fbox{ヌ}}\;\right)^n\sin\left(\frac{n\pi}{\fbox{ネ}}\right)
  $$となる。また，$a_1,\cdots, a_{100}$ のうち $a_n$ が最大となるのは $n=\fbox{ノハ}, \fbox{ヒフ}$ のときである。ただし $\fbox{ノハ} < \fbox{ヒフ}$ とする。

※この問題では，数列とは写像 $a: \mathbb{N} \to \mathbb{C}$ のことをいう。$n\in\mathbb{N}$ に対して，$a(n)$ のことを単に $a_n$ と表記する。また，記号の濫用であるが $a$ を $\{a_n\}, a_n$とも書く。

解答形式

空欄 $\fbox{ア}$ 〜 $\fbox{フ}$ には，半角数字 0 - 9 または記号 - のいずれかが当てはまります。$\fbox{ア}$ 〜 $\fbox{フ}$ に当てはまるものを改行区切りで入力してください。

問題文

$\displaystyle f(x)=\int_{0}^{1}\frac{(1+xt^2)-e^{xt^2}}{t\cdot e^{xt^2}}dt$とおく。
1 $\displaystyle \lim_{x \to 0}\frac{f(x)}{x^p}$が有限値となる$p$とその極限値$\alpha$を求めよ。
2 $\displaystyle \lim_{x \to \infty}\frac{f(x)}{(\log{x})^q}$が有限値となる$q$とその極限値$\beta$を求めよ。

解答形式

$p=\fbox{ア}$
$\alpha=\displaystyle-\frac{\fbox{イ}}{\fbox{ウ}}$
$q=\fbox{エ}$
$\beta=\displaystyle-\frac{\fbox{オ}}{\fbox{カ}}$
である。$\fbox{ア}$から順に1行ごとに答えよ。

問題文

行列$A$を次で定義する。
$$
A=
\begin{pmatrix}
6& -3 & -7 & 0 & 0 & 0\\
-1 & 2 & 1 & 0 & 0 & 0\\
5& -3 & -6 & 0 & 0 & 0\\
0& 0 & 0 & 1 & 2 & 1\\
0& 0 & 0 & -1 & 4 & 1\\
0& 0 & 0 & 2 & -4 & 0\\
\end{pmatrix}
$$
このとき次の実線形空間の次元を求めよ。
$$
V=\{X\in M_{6}(\mathbb{R})\mid AX=XA\}
$$
ただし、$M_{6}(\mathbb{R})$とは6行6列の実正方行列全体の集合である。

解答形式

半角数字で答えよ。

問題文

$$
\newcommand{\nc}{\newcommand}
\nc{\wake}[1]{\begin{cases} #1 \end{cases}}
\nc{\f}[2]{\dfrac{#1}{#2}}
\nc{\s}[1]{\{#1\}}
\nc{\pmat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\nc{\lr}[1]{\left( #1 \right)}
\nc{\com}[2]{{}_{#1}{\rm C}_{#2} \right)}
\nc{\bar}[1]{{\overline{#1}}}
\nc{\bb}[1]{{\mathbb {#1}}}
\nc{\rmn}[1]{{\rm #1}}
\nc{\q}{\quad}
\nc{\x}{\times}
\nc{\a}{\alpha}
\nc{\b}{\beta}
\nc{\th}{\theta}
\nc{\Q}[1]{\fbox{#1}}
$$

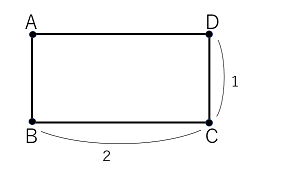
下のように $\rm AB=1\ ,\ BC=2$ の長方形 $\rm ABCD$ がある。点 $\rm P$ は $t=0$ で点 $\rm A$ におり、 $1$ 秒間に $1$ の速度で辺の上を進む。点 $\rm P$ が 点 $\rm A,B,C,D$ のいずれかにいるとき確率 $p$ で辺 $\rm AB$ に平行な向きに、 $1-p$ の確率で辺 $\rm AD$ に平行な向きに向きを変え、それ以外の場所で向きを変えることはないものとする。

$p=\dfrac56$ とするとき点 $\rm P$ が $2n$ 秒後 $(n=0,1,2,\cdots)$ に点 $\rm A$ にいる確率を求めたい。

点 $\rm P$ が $2n$ 秒後に点 $\rm A,D$ にある確率を $A_n,D_n$ とおく。このとき $X_n=A_n+D_n$ とおくと漸化式
$$
X_{n+1}=\f{\Q{ア}}{\Q{イ}}X_n +\f{\Q{ウ}}{\Q{エ}}
$$
が成り立つ。また $Y_n=A_n-D_n$ とおくと漸化式
$$
Y_{n+2}-\f{\Q{オ}}{\Q{カ}}Y_{n+1}+\f{\Q{キ}}{\Q{ク}}Y_n=0
$$
が成り立つ。これらを初期条件 $X_0=\Q ケ\ ,Y_0=\Q{コ}\ ,Y_1=\f{\Q{サ}}{\Q{シ}}$ のもとで解くことで
$$
A_n=\f{\Q ス}{\Q セ}+\f{\Q ソ}{\Q タ}\lr{\f{\Q チ}{\Q ツ}}^n-\lr{\f{\Q テ}{\Q ト}}^n+\f{\Q ナ}{\Q ニ}\lr{\f{\Q ヌ}{\Q ネ}}^n
$$
を得る。なお ${\f{\Q チ}{\Q ツ}}<{\f{\Q ヌ}{\Q ネ}}$ である。

解答形式

上の空欄を埋めよ。解答は半角数字・改行区切りで入力すること。ただし $\Q ア$ から $\Q ネ$ にはそれぞれ 1 から 999 までの整数が入り、分数は既約分数の形で表してある。

問題文

$n$ を正の整数とするとき，以下の条件を満たす三角形の総数 $T_n$ を求めなさい。ただし，互いに合同であるような $2$ つの三角形は区別しない。

• 条件：三角形の辺の長さはすべて $n$ 以下の整数である。

例えば，$n=1$ のときには，辺の長さが $1$ の正三角形を作ることができる。これ以外に条件を満たすような三角形は存在しない。よって $T_1=1$ である。

$n$ が奇数のとき

$$
T_n=\frac{\fbox{ア}}{\fbox{イウ}}n^3+\frac{\fbox{エ}}{\fbox{オ}}n^2+\frac{\fbox{カ}}{\fbox{キク}}n+\frac{\fbox{ケ}}{\fbox{コ}}
$$

である。

解答形式

空欄 $\fbox{ア}$ 〜 $\fbox{コ}$ には，半角数字 0 - 9 ，記号 - のいずれかが当てはまります。$\fbox{ア}$ 〜 $\fbox{コ}$ に当てはまるものを改行区切りで入力してください。分数は既約分数の形で答えてください。

問題文

相異なる正の実数 $a,b,c$ が $ab^2(1-b)=bc^2(1-c)=ca^2(1-a)$ を満たして動くとき、$(1-a)(1-b)(1-c)$ の最大値は

$$
\displaystyle \frac{\fbox{アイウ}+\fbox{エオ}\sqrt{\fbox{カ}}}{\fbox{キクケ}}
$$

である。

解答形式

ア〜ケには、0から9までの数字、または-（マイナス）が入る。文字列「アイウエオカキクケ」を全て半角で1行目に入力せよ。ただし、それ以上約分できない形で、かつ根号の中身が最小になるように答えよ。

問題文

しずかちゃんがシャワーを浴びようとしてお湯を出し始めた。はじめのお湯の温度は $35$℃で、お湯を出し始めてから $n$ 秒後のお湯の温度は $T_n$℃であるとする。

しずかちゃんは非常に温度に敏感で、シャワーの温度をちょうど $40$℃に設定しないと落ち着かない。そこで、しずかちゃんはお湯を出し始めてから $n=1,2,3...$ 秒後に、シャワーの温度がちょうど $a(40-T_n)$℃だけ上がるように温度調節レバーを操作する。ここで、$a$ は正の定数である。なお、$T_n>40$ のときは $a(T_n-40)$℃だけ温度が「下がる」ように操作するものとする。

$N$ を自然数の定数として、温度調節レバーの操作がお湯の温度に反映されるまでちょうど $N$ 秒かかる。すなわち、しずかちゃんがお湯を出し始めてから $n$ 秒後に温度調節レバーを操作したとき、 はじめから $n+N$ 秒後と $n+N+1$ 秒後の間にシャワーの温度が $a(40-T_n)$℃だけ上昇する。

さて、$\displaystyle \lim_{n \to \infty} T_n=40$ であれば、しずかちゃんは十分な時間が経つと快適にシャワーを浴びることができる。$a$ が十分小さければ、すなわち温度をできるだけ少しづつ上げていけば、直感的にはこのことは可能である。では、具体的には $a$ はどれほど小さい必要があるのだろうか。そこで、$\displaystyle \lim_{n \to \infty} T_n=40$ が成り立たないような $a$ の最小値を $a_c$ とおく。以下の空欄を埋めよ。

（１） $N=1$ のとき、$a_c=\fbox{ア}$ である。

（２） $N=2$ のとき、$\displaystyle a_c=\frac{\fbox{イウ}+\sqrt{\fbox{エ}}}{\fbox{オ}}$ である。

解答形式

ア〜オには、0から9までの数字または「-」(マイナス)が入る。
（１）の答えとして「ア」にあてはまる数を半角で1行目に入力せよ。
（２）の答えとして、文字列「イウエオ」を半角で2行目に入力せよ。

問題文

数列$~\{a_n\},~\{b_n\}$を相異なる2つの実数$~\alpha,\beta~$を用いて以下のように定義する。
$$
a_n = \cfrac{1}{\displaystyle{\sum_{k=0}^n}\alpha^{n-k}\beta^{k}}~~~,~~~b_n = \sum_{m=0}^\infty\frac{1}{a_mn^{m+2}}
$$ただし、$\{b_n\}~$は$n\geq 2$で定義されるものとする。$\alpha,\beta~$が
$$
\begin{cases}
\alpha + \beta = 1\\
|\alpha||\beta| = 1
\end{cases}
$$を満たすとき、
$$
a_k = b_k
$$となる最小の自然数$~k~$は$~k=\fbox{ア}\fbox{イ}$であり、このとき$~b_k = \cfrac{\fbox{ウ}}{\fbox{エ}\fbox{オ}}$である。

解答形式

ア〜オには0から9までの数字のいずれかが入る。
数字列「アイウエオ」をすべて半角で入力し解答せよ。
ただし、分数は既約分数の形にすること。

問題文

$a,b$を$a>1,b>1$を満たす実数とする。
$\theta$が$0\leq\theta<2\pi$の範囲を動くとき$f(\theta)=\sqrt{a^2-2a\cos\theta+1}+\sqrt{b^2-2b\sin\theta+1}$の最小値が$\sqrt{a^2+b^2}$となるような$(a,b)$の存在範囲を$ab$平面に図示したとき、その領域の面積を求めよ。

解答形式

整数または既約分数で答えてください。
半角で入力してください。