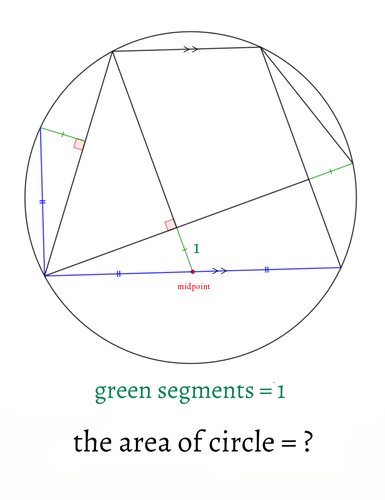
[D] 円が線になるまで
解答
(1)1
(2)3111411
(3)2125
解説
以下、$i$ を虚数単位とする。
(1)$\alpha=0$ のとき、$D$ を定める式は $|z|\leq 1$ であり、これは複素数平面上で原点を中心とする半径 $1$ の円の周上および内部を表す。
(2)$|\alpha|=1$ のとき、$\alpha=\cos\theta + i\sin\theta\ \ (0\leq \theta <2\pi)$ とおいて考察する。
$D$ を定める式は $z=\alpha\bar{z}$ である。$\alpha=\cos\theta + i\sin\theta$ とおく。原点 $z=0$ が $D$ に含まれることは明らかなので、それ以外を $z=r(\cos\phi + i\sin\phi)\ \ (r>0)$ とおいて調べる。$\alpha,z$ の表式を $z=\alpha\bar{z}$ に代入すると
$$
\begin{eqnarray}
&&r(\cos\phi + i\sin\phi) = (\cos\theta + i\sin\theta)\cdot r(\cos\phi - i\sin\phi) \\
\Leftrightarrow&& \cos\phi + i\sin\phi = (\cos\theta + i\sin\theta)(\cos\phi - i\sin\phi) \\
\Leftrightarrow&&\cos\phi + i\sin\phi = (\cos\theta\cos\phi +\sin\theta\sin\phi) + i(\sin\theta\cos\phi -\cos\theta\sin\phi) \\
\Leftrightarrow&&\cos\phi + i\sin\phi = \cos(\theta-\phi) + i \sin(\theta-\phi) \\
\end{eqnarray}
$$
最後の式で両辺の偏角が一致するので、$z\neq 0$ が $D$ に属するための必要十分条件は、ある整数 $n$ を用いて $\displaystyle \phi=\theta-\phi + 2n\pi \Leftrightarrow \phi=\frac{\theta}{2}+n\pi$ と書けることである。$0\leq \theta <2\pi$ なので、$0\leq \phi <2\pi$ の範囲で条件を満たす $n$ は $n=0,1$ で
$$
\phi=\frac{\theta}{2},\frac{\theta}{2}+\pi
$$
である。特に $\theta =\displaystyle \frac{6}{11}\pi$ のとき、
$$
\phi=\frac{3}{11}\pi,\frac{14}{11}\pi
$$
であり、$z=0$ も $D$ に含まれることと併せると、$D$ は傾き $\tan\phi=\tan \displaystyle \left(\frac{3}{11}\pi\right)$ の直線であることがわかる。
(3)$0<|\alpha|<1$ のとき、$\alpha=q(\cos\theta + i\sin\theta)\ \ (0<q<1,\ 0\leq \theta <2\pi)$ とおく。この場合も原点 $z=0$ が $D$ に含まれることは明らかなので以下 $z\neq 0$ とする。$\displaystyle \phi=\frac{\theta}{2}$ とおき、 $w=z(\cos\phi - i\sin\phi)\Leftrightarrow z=w(\cos\phi + i\sin\phi)$ と定めると $\bar{z}=\bar{w}\cdot (\cos\phi - i\sin\phi)$ であり、
$$
\begin{eqnarray}
|z- \alpha\bar{z}|&=& |w(\cos\phi + i\sin\phi)- q(\cos\theta + i\sin\theta)\cdot\bar{w}(\cos\phi - i\sin\phi) | \\
&=&|w(\cos\phi + i\sin\phi)- q(\cos\phi+ i\sin\phi)\cdot\bar{w}| \\
&=&|\cos\phi + i\sin\phi|\cdot|w- q\bar{w}| \\
&=&|w- q\bar{w}|
\end{eqnarray}
$$
と変形できる。よって、$z=w=0$ のときも併せると、$z\in D$ は $w$ が $|w- q\bar{w}| \leq 1-q^2$ を満たすことと同値である。この条件を $w=x+yi$ ($x,y$ は実数) とおいて同値変形すると
$$
\begin{eqnarray}
|w- q\bar{w}| &\leq& 1-q^2\\
\Leftrightarrow |(x+yi)- q(x-yi)|&\leq& 1-q^2 \\
\Leftrightarrow |(1-q)x+(1+q)yi)|&\leq& 1-q^2 \\
\Leftrightarrow \sqrt{(1-q)^2x^2+(1+q)^2y^2}&\leq& 1-q^2 \\
\Leftrightarrow (1-q)^2x^2+(1+q)^2y^2&\leq& (1-q^2)^2 \\
\Leftrightarrow \frac{x^2}{(1+q)^2}+\frac{y^2}{(1-q)^2}&\leq& 1 \\
\end{eqnarray}
$$
である。これは半長軸の長さが $1+q$ (実軸方向)で、半短軸の長さが $1-q$ (虚軸方向)であるような楕円の周上および内部を表す。$z$ は $w$ を原点を中心として反時計回りに $\displaystyle \phi=\frac{\theta}{2}$ 回転させた複素数であったから、$D$ はこの楕円の周上および内部を原点を中心として反時計回りに $\displaystyle \phi=\frac{\theta}{2}$ 回転させたものとなる。回転によって面積は変わらないので、$D$ の面積は回転させる前の楕円の面積に等しく、$(1+q)\cdot(1-q)\cdot\pi=(1-q^2)\pi$ である。特に $q=0.4$ のとき、
$$
(1-0.4^2)\pi=\frac{21}{25}\pi
$$
である。
補足
本問で考察した $|\alpha|\leq1$ かつ $|z- \alpha\bar{z}|\leq1-|\alpha|^2$ という条件は、実は複素数 $\zeta$ の $2$ 次方程式 $\zeta^2 + z\zeta +\alpha =0$ の $2$ つの複素数解がいずれも $|\zeta|\leq 1$ を満たす条件と同値です。より一般化された場合の主張は Lehmer–Schur algorithm として知られています (https://en.wikipedia.org/wiki/Lehmer%E2%80%93Schur_algorithm, 2025年7月18日アクセス)。
おすすめ問題
この問題を解いた人はこんな問題も解いています