数学の問題一覧
問題文
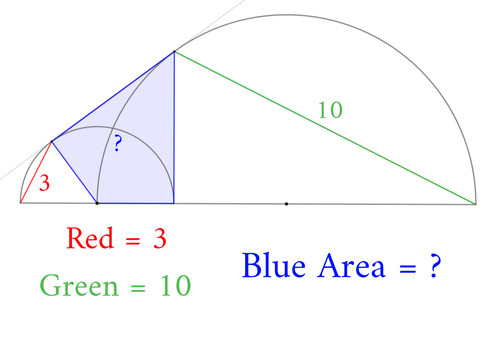
図のように2つの半円が配置されています。(右側の半円の直径の一端は左側の半円の中心に一致する。)赤、緑で示した線分の長さがそれぞれ3,10のとき、青で示した四角形の面積を求めてください。
ただし、図中点線で示した直線は2つの半円の共通接線です。
解答形式
半角数字で解答してください。
問題文
$x$の4次方程式
$$
x^{4}-5x^{3}-2(n+7)x^{2}+5nx+n^{2}=0
$$が異なる4つの整数解をもつとき、整数$n$の値を求めよ。
解答形式
半角数学で解答してください。
また、$n$の値が2つ以上ある場合
改行して小さい順に並べてください。
(例) $n= -5 , -4$ のとき
-5
-4

【補助線主体の図形問題 #032】
3連休の中日になりそこなった日曜の出題はこんな問題にしてみました。今週も変わらず方針・補助線次第で暗算処理可能です。お好きなタイミングで図形問題と戯れてみてください。
解答形式
${\def\cm{\thinspace \mathrm{cm}}}$ 解答は小数第3位を四捨五入して、小数第2位までを単位なしで入力してください。
(例) $12\cm$ → $\color{blue}{12.00}$ $10\sqrt{2}\cm$ → $\color{blue}{14.14}$ $\dfrac{1+\sqrt{5}}{2} \cm$ → $\color{blue}{1.62}$
入力を一意に定めるための処置です。
たとえば答えに無理数を含む場合、$\sqrt{2}=1.41$や$\pi=3.14$などでは必要な桁が足りない場合があるのでご注意ください。
近似値を求める際には、関数電卓やグーグルの電卓機能、Wolfram|Alpha https://www.wolframalpha.com などのご利用をお勧めします。
問題文
$n$を2以上の整数とし, $f(x)=\sqrt[n]{x^n+nx^{n-1}} (x\geq0)$を考える。
$(1)$ $x$を正の整数とするとき, $f(x)$の値が整数でないことを示せ。
$(2)$ $y=f(x)$, $x$軸, $x=m-1$ ($m$は正の整数) で囲まれた領域内(境界線上も含む)の格子点の数を求めよ。
解答形式
$(2)$ で $m=100$ のときの答えを半角数字で入力してください。
問題文
(1)$2024!$は何回$2$で割り切ることができるか答えよ。
(2)$[\sqrt{2024}]$、$[\sqrt[3]{2024}]$の値を求めよ。ただし、$[x]$は$x$を超えない最大の整数を表すものとする。
チャレンジ課題
(3)$2024!$の約数の個数は$10^{91}$より大きいことを示せ。ただし、$1$から$2024$までの素数は$306$個である。
解答形式
(1) ~~~
(2) ~~~
の形でお願いします。問題番号と解答、一つの小問の解答と解答の間は半角スペースを開けてください。
解答は数字のみお書きください。
問題文
垂心を$H$とする鋭角三角形$ABC$があり、$AB=9,AC=11,CH=7$を満たしています。
$△AHC$の外接円を$Γ$とし、直線$BH$と$Γ$の交点のうち$H$でない点を$D$として、線分$CD$の中点を$M$とします。
線分$HM$と線分$AC$の交点を$E$としたときの、$DE$の長さの$2$乗を求めてください。
解答形式
求める値は互いに素な整数$a,b$を用いて$\dfrac{a}{b}$と表されるので、$a+b$を解答してください。
問題文
鋭角三角形 $ABC$ について,垂心を $H$,外心を $O$,直線 $CH$ と直線 $AB$ の交点を $F$,直線 $BC, AC$ について $F$ と対称な点をそれぞれ $X, Y$ とし,直線 $BX$ と直線 $AY$ の交点を $P$ とします.$\angle FOX=\angle AFP$ かつ $FH=1, HC=7$ が成り立つとき,円 $ABC$ の半径としてありうる値の二乗の総和は互いに素な正整数 $a, b$ を用いて $\dfrac{a}{b}$ と表せるので,$a+b$ を解答してください.
問題文
扇形内部に図のように線を引きました。青い三角形の面積が12のとき、緑の三角形の面積を求めてください。

解答形式
半角数字で解答してください。
