問題文
2つの正方形が図のように配置されています。赤い線分の長さが4のとき、2つの正方形の面積の合計を求めてください。

解答形式
半角数字で解答してください。
問題文
2021.3.21 22:28 問題タイトルを修正しました。(解答に影響はありません)
正三角形の内接円と外接円があります。図のように線分の長さが与えられたとき、正三角形の一辺の長さを求めてください。

解答形式
答えは$\fbox ア\sqrt{\fbox イ}$となります。文字列 アイ を解答してください。
ただし、$\fbox ア,\fbox イ$には一桁の自然数が入ります。また、根号の中身が平方数の倍数にならないように解答してください。
問題文
2つの合同な長方形を図のように配置しました。赤い三角形の面積が10のとき、青い凹四角形の面積を求めてください。

解答形式
半角数字で解答してください。
問題文
内接四角形ABCDとその対角線の交点Mについて、図のような条件が与えられたとき、線分ACの長さを求めてください。

解答形式
半角数字で解答してください。
問題文
図のように正五角形と正三角形が配置されています。緑の$x$で示した角度を求めてください。
なお、赤で示した2つの線分は長さが等しく、青で示した角は直角です。

解答形式
度数法で、単位を付けずに0以上180未満の数を半角数字で解答してください。
問題文
(2021.3.13 15:56 追記) 解答に誤りがあったため修正しました。
次の不等式を満たす最大の自然数$n$を求めてください。
$$
2^{n+1}-10\sum_{k=1}^n \lfloor \frac{2^{k-1}}{5} \rfloor \le 20210220
$$ただし、$\lfloor x\rfloor$は$x$を超えない最大の整数を表します。
解答形式
半角数字で解答してください。
問題文
半径21の扇形に図のように線を引きました。青い三角形の面積が213のとき、赤い線分の長さを求めてください。
※高校数学カテゴリに入れてますが、中学数学範囲での綺麗な解法をTwitterにて頂きました。是非考えてみてください。
解答形式
解答は既約分数$\frac{\fbox{アイウ}}{\fbox{エ}}$となります。文字列「アイウエ」を解答してください。
ただし、$\fbox ア ~ \fbox エ$には$0$以上$9$以下の整数が入ります。
問題文
正方形の中に図のように線を引きました。赤、青の線分の長さがそれぞれ1,7のとき、緑の線分の長さを求めてください。

解答形式
半角数字で解答してください。
問題文
長方形・正方形・円が図のように配置されています。赤で示した線分の長さが7、長方形の面積が12のとき、青い線分の長さとしてあり得るものを全て求めてください。

解答形式
解答は$\sqrt{\fbox {アイ}},\frac{\sqrt{\fbox{ウエオ}}}{\fbox カ}$となります。文字列「アイウエオカ」を解答してください。ただし、根号の中身が平方数の倍数とならないように解答してください。
問題文
図のように3つの正方形が配置されています。3つの線分の長さが図のように与えられたとき、緑の六角形の面積を求めてください。

解答形式
面積は、
$$
\fbox{アイ}+\frac{\fbox{ウエ}\sqrt{\fbox{オカ}}}{\fbox{キ}}
$$
となります。$\fbox ア~\fbox キ$には0以上9以下の整数が入ります。文字列「アイウエオカキ」を解答してください(「」は不要)。ただし、根号の中身や分数は最も簡単な形にしてください。
例$$
面積S=17+\frac{22\sqrt{52}}{8}\rightarrow 17+\frac{11\sqrt{13}}{2}\rightarrow 1711132 と解答
$$
問題文
$x,y,z$は全て正の実数とします。次式で定義される$f(x,y,z)$について、次の値を求めてください。$$f(x,y,z)=\frac{1+x^2}{y+z}+\frac{1+y^2}{z+x}+\frac{1+z^2}{x+y}$$
$(1)$ $f(x,y,z)$の最小値
$(2)$ $x+y+z=1$のとき、$f(x,y,z)$の最小値
$(3)$ $x^2+y^2+z^2=1$のとき、$f(x,y,z)$の最小値
解答形式
$(1)$の答えは$\fbox ア$、$(2)$の答えは$\fbox イ$、$(3)$の答えは$\fbox ウ\sqrt{\fbox エ}$です。
文字列「アイウエ」を解答してください。
問題文
緑色の五角形の面積を求めてください。
紫でしめした3つの角は等しく、赤同士、青同士の線分はそれぞれ等しい長さです。
解答形式
半角数字で解答してください。
問題文
次の文章の空欄を埋めてください。ただし、以下の文章全てにおいて$x>0$とします。
$(1.1)$
$f(x)=x+4x^{-2}$の最小値を、微分を用いて求めよう。まず、
$$f'(x)=\fbox ア-\frac{\fbox イ}{x^3}$$である。$f'(x)$の符号は$x=\fbox ウ$の前後でのみ変化するから、$f(x)$は$x=\fbox ウ$で極値をとり、さらにそれが最小値であることが分かる。したがって、$f(x)$の最小値は$\fbox エ$である。
この問題は$(1.2)$に示すような解法が知られている。
$(1.2)$
相加相乗平均の関係式を用いて$f(x)$の最小値を求める。$a_1+a_2=1$を満たす$0$以上の実数$a_1,a_2$を用いて、
$$f(x)=a_1x+a_2x+\frac{4}{x^2}\ge3\left(a_1x\cdot a_2x\cdot\frac{4}{x^2}\right)^{\frac 13}=3(4a_1a_2)^{\frac 13}$$とする。いかなる$a_1,a_2$の組に対してもこの不等式は成立する。一方で、等号を成立させる$x$が存在するには、$a_1x=a_2x$でなければならないから、$a_1=a_2$となる。このとき、等号成立条件
$$a_1x=a_2x=\frac{4}{x^2}$$を満たす$x$は存在して、その値は$x=\fbox ウ$で、不等式の右辺の値は$\fbox エ$となり、最小値が得られる。
$(2)$
$g(x)=x+3x^{-1}+x^{-2}$の最小値を、$(1.2)$の解法に準じて求めよう。
$(1.2)$中の議論と同様に、等号成立条件を考えれば、同類項の係数(前問では$a_1,a_2$にあたる)が異なってはならないと言える。したがって、$3$つの自然数$b_1,b_2,b_3$を用いて、$$g(x)=b_1\cdot \frac{x}{b_1}+b_2\cdot\frac{3}{b_2x}+b_3\cdot\frac{1}{b_3x^2}$$と考えることにする(即ち、$b_1$個の$x/b_1$、$b_2$個の$3/b_2x$、$b_3$個の$1/b_3x^2$の和と考える)。相加相乗平均の関係式を適用したときに、累乗根の中身が定数となるには、$b_1=\fbox オb_2+\fbox カb_3$であればよい。等号成立条件は$$\frac{x}{b_1}=\frac{3}{b_2x}=\frac{1}{b_3x^2}$$である。中辺と最右辺の等式から、$x=b_2/(3b_3)$であり、これと最左辺・最右辺の等式から、$$\frac{b_2}{3b_3\left(\fbox オb_2+\fbox カb_3\right)}=\frac{9b_3}{b_2^2}$$整理して、$$b_2^3-\fbox{キク}b_2b_3^2-\fbox{ケコ}b_3^3=0$$この式を解くと、$b_2/b_3=\fbox サ/\fbox シ$を得られるので、$b_1:b_2:b_3=\fbox ス:\fbox セ:\fbox ソ$であれば良いことが分かる。これより、$$g(x)\ge\left(b_1+b_2+b_3\right)\left(\left(\frac{x}{b_1}\right)^{b_1}\left(\frac{3}{b_2x}\right)^{b_2}\left(\frac{1}{b_3x^2}\right)^{b_3}\right)^{\frac{1}{b_1+b_2+b_3}}=\frac{\fbox{タチ}}{\fbox ツ}$$であり、$x=\fbox テ$で等号が成立して、最小値となる。
解答形式(要注意!)
以下のこと(特に2つ目)に注意して解答してください。
・$\fbox ア~\fbox テ$には$0$以上$9$以下の整数が入ります。
・式の係数・分母の空欄$\left(\fbox オ・\fbox カ・\fbox シ・\fbox ツ\right)$には$1$が入る可能性もあります。
・$\fbox ス~\fbox ソ$は、$\fbox ス+\fbox セ+\fbox ソ$が最小となるようにしてください。また、分数は既約分数にしてください。
文字列アイウエを$1$行目
文字列オカキクケコを$2$行目
文字列サシスセソを$3$行目
文字列タチツテを$4$行目
に入力して解答してください。
問題文
長方形$ABCD$を底面とする四角錐$P-ABCD$があります。$PA=1,PB=4,PC=8$のとき、$PD$の長さを求めてください。

解答形式
半角数字で解答してください。
問題文
次の文章の空欄を埋めてください。
$n$個の実数$x_1,x_2,\cdots,x_n$が、$x_1+2x_2+3x_3+\cdots+nx_n=n$を満たすとき、$x_1^2+x_2^2+\cdots+x_n^2$の最小値を$m_n$とすると、
$$
m_n=\frac{\fbox アn}{(n+\fbox イ)(\fbox ウn+1)}
$$
であり、
$$
\lim_{n\rightarrow\infty}\left(m_1+\frac{m_2}{2}+\cdots+\frac{m_n}{n}\right)=\fbox{エオ}\left(-\frac{1}{\fbox カ}+\ln{\fbox キ}\right)
$$
である。
解答形式
$\fbox ア~\fbox キ$には$1$以上$9$以下の整数が入ります。文字列アイウエオカキを半角数字で解答してください。
例: $\fbox ア=1,\fbox イ=2,\fbox ウ=3,\fbox {エオ}=45,\fbox カ=6,\fbox キ=7$ $\rightarrow$ $1234567$ と解答
問題文
周の長さが30である長方形ABCDがあります。辺CD上に∠APB=90°となるような点Pをとれるとき、長方形ABCDの面積の最大値を求めてください。
解答形式
半角数字で解答してください。
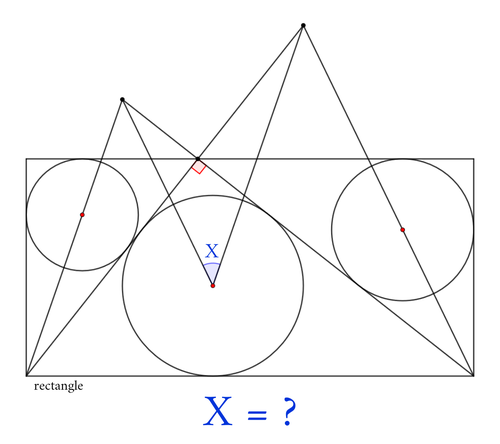
問題文
図のように長方形や直角三角形の内接円が配置されています。青で示した角の角度を求めてください。
解答形式
度数法で求め、半角数字で0以上360未満の整数を解答してください。
※度や°などの単位は付けないでください。
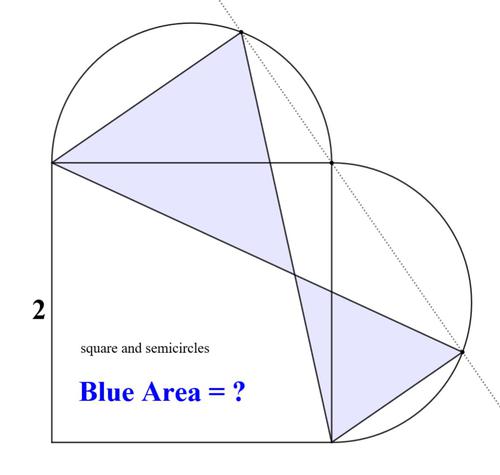
問題文
図のように正方形・半円が配置されています。正方形の一辺の長さが2であるとき、青で示した部分の面積(の合計)を求めてください。
解答形式
半角数字で解答してください。